题目内容
19.已知命题p:方程x2-4x+m=0有实根,命题q:-1≤m≤5.若p∧q为假命题,p∨q为真命题,求实数m的取值范围.分析 求出p为真时的m的范围,结合p∧q为假命题,p∨q为真命题,通过讨论p,q的真假,得到关于m的不等式组,解出即可.
解答 解:p为真命题?△=16-4m≥0,
∴m≤4--------------------------------------(3分),
∵p∧q为假命题,p∨q为真命题,
∴p,q一真一假--------------------(4分)
当p真q假时,$\left\{\begin{array}{l}m≤4\\ m<-1或m>5\end{array}\right.$,
∴m<-1------------------------------(7分)
当p假q真时,$\left\{\begin{array}{l}m>4\\-1≤m≤5\end{array}\right.$,
∴4<m≤5-------------------------------(9分)
综上所述,实数m的取值范围是:(-∞,-1)∪(4,5]----------------------(10分)
点评 本题考查了复合命题的判断,考查二次方程问题,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知等差数列{an},{bn}的公差分别是p,q(pq≠0),则数列{an+bn}( )
| A. | 是公差为p的等差数列 | B. | 是公差为q的等差数列 | ||
| C. | 是公差为p+q的等差数列 | D. | 不是等差数列 |
7.f(x)=sin(x-α),f(x)在〔0,$\frac{π}{3}$〕上的定积分等于0,则tanα=( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{1}{{\sqrt{3}}}$ | D. | -$\frac{1}{{\sqrt{3}}}$ |
14.函数y=2016x-sinx的图象大致是( )
| A. | 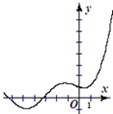 | B. | 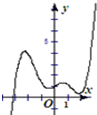 | C. | 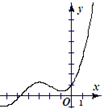 | D. | 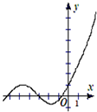 |
4.设A={小于90°的角},B={第一象限角},则A∩B等于( )
| A. | {锐角} | B. | {小于90°的角} | ||
| C. | {第一象限角} | D. | {α|k•360°<α<k•360°+90°(k∈Z,k≤0)} |
9.若a<b≤0,则2a-b-$\frac{1}{a(a-b)}$=( )
| A. | 最小值-$\frac{1}{3}$ | B. | 最大值-$\frac{1}{3}$ | C. | 最大值-3 | D. | 最小值-3 |
 设函数f(x)=|log2(x+2)|-1.
设函数f(x)=|log2(x+2)|-1.