题目内容
6.若△ABC中三个内角A,B,C的对边分别为a,b,c,且$\frac{1+cosB}{sinA}$=$\frac{\sqrt{3}b}{a}$.(1)求角B;
(2)点D为BC的中点,AD=$\frac{\sqrt{3}}{2}$,BC=$\frac{6}{5}$,且sin∠BAD=$\frac{3}{5}$,求AC.
分析 (1)根据正弦定理和已知条件可得$\frac{1+cosB}{\sqrt{3}}=sinB$,从而计算出B;
(2)在△ABD和△ABC中依次使用余弦定理求出AB,AC.
解答 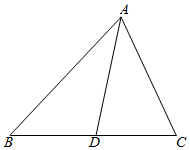 解:(1)∵$\frac{1+cosB}{sinA}$=$\frac{\sqrt{3}b}{a}$,∴$\frac{a}{sinA}=\frac{b}{\frac{1+cosB}{\sqrt{3}}}$,
解:(1)∵$\frac{1+cosB}{sinA}$=$\frac{\sqrt{3}b}{a}$,∴$\frac{a}{sinA}=\frac{b}{\frac{1+cosB}{\sqrt{3}}}$,
又由正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}$,
∴$\frac{1+cosB}{\sqrt{3}}=sinB$.即$\sqrt{3}$sinB-cosB=1,sin(B-$\frac{π}{6}$)=$\frac{1}{2}$,
∴-$\frac{π}{6}$<B-$\frac{π}{6}$$<\frac{5π}{6}$,∴B-$\frac{π}{6}$=$\frac{π}{6}$
∴B=$\frac{π}{3}$.
(2)在△ABD中,由余弦定理得:cosB=$\frac{A{B}^{2}+B{D}^{2}-A{D}^{2}}{2AB•BD}$=$\frac{A{B}^{2}+\frac{9}{25}-\frac{3}{4}}{\frac{6}{5}AB}$=$\frac{1}{2}$.
解得AB=$\frac{3+4\sqrt{3}}{10}$.
在△ABC中,由余弦定理得:AC=AB2+BC2-2AB•BCcosB=($\frac{3+4\sqrt{3}}{10}$)2+$\frac{36}{25}$-2×$\frac{6}{5}×$$\frac{3+4\sqrt{3}}{10}$×$\frac{1}{2}$=$\frac{165-24\sqrt{3}}{100}$.
∴AC=$\frac{\sqrt{165-24\sqrt{3}}}{10}$.
点评 本题考查了正弦定理,余弦定理,属于中档题.

| A. | $-\frac{1}{3}$ | B. | 1 | C. | 2 | D. | $-\frac{1}{2}$ |
| A. | 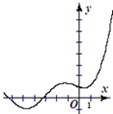 | B. | 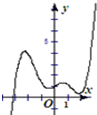 | C. | 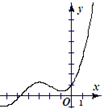 | D. |  |
| A. | 2 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |