题目内容
3.等差数列{an}中,若a3=5,则a1+2a4=15.分析 设{an}的首项为a1,公差为d,由等差数列的通项公式可得a1+2d=5,进而分析可得a1+2a4=a1+2(a1+3d)=3(a1+2d),代入数据计算可得答案.
解答 解:根据题意,设{an}的首项为a1,公差为d,
若a3=5,则a1+2d=5,
那么a1+2a4=a1+2(a1+3d)=3(a1+2d)=3×5=15;
故答案为:15.
点评 本题考查等差数列的通项公式的运用,关键是充分利用等差数列的通项公式分析(a1+2a4)与a3的关系.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
14.函数y=2016x-sinx的图象大致是( )
| A. | 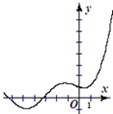 | B. | 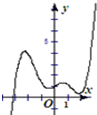 | C. | 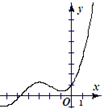 | D. | 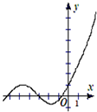 |
15.已知在等比数列{an}中,Sn是{an}的前n项和,a1+a3=10,S4=15,则该数列的公比等于( )
| A. | 2 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
12.函数f(x)=sinωx(ω>0)在区间(-$\frac{2π}{3}$,$\frac{π}{3}$)上有且只有2个极值点,则ω的取值范围是( )
| A. | [$\frac{3}{2}$,$\frac{9}{4}$] | B. | ($\frac{3}{2}$,$\frac{9}{4}$) | C. | ($\frac{3}{2}$,$\frac{9}{4}$] | D. | [$\frac{3}{2}$,$\frac{9}{4}$) |
2.已知a,b,c分别为△ABC三个内角A,B,C的对边,a=2,A=60°,则△ABC面积的最大值为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |