题目内容
9.若等比数列{a${\;}_{{n}_{\;}}$}的公比为q(q≠0),则关于x、y的二元一次方程组$\left\{\begin{array}{l}{{a}_{1}x+{a}_{3}y=3}\\{{a}_{2}x+{a}_{4}y=-2}\end{array}\right.$的解的情况的下列说法中正确的是( )| A. | 对任意q∈R(q≠0),方程组都有唯一解 | |
| B. | 对任意q∈R(q≠0),方程组都无解 | |
| C. | 当且仅当q=-$\frac{2}{3}$时,方程组有无穷多解 | |
| D. | 当且仅当q=-$\frac{2}{3}$时,方程组无解 |
分析 先消元,再根据等比数列的性质得到,0•x=3a4+2a3,问题得以解决.
解答 解:解方程组$\left\{\begin{array}{l}{{a}_{1}x+{a}_{3}y=3}\\{{a}_{2}x+{a}_{4}y=-2}\end{array}\right.$,消y得到(a1a4-a2a3)x=3a4+2a3,
∵等比数列{a${\;}_{{n}_{\;}}$}的公比为q,
∴a1a4-a2a3=0,
当3a4+2a3,=0时,即q=-$\frac{2}{3}$时,方程组有无穷多解,
故选:C.
点评 本题以方程组的解为载体,考查等比数列的性质,属于基础题.

练习册系列答案
相关题目
19.在同一坐标系中,函数y=3-x与y=3x的图象之间的关系是( )
| A. | 关于原点对称 | B. | 关于直线y=x对称 | C. | 关于x轴对称 | D. | 关于y轴对称 |
17.若点P(x,y)为不等式组$\left\{\begin{array}{l}2x-y-2≥0\\ x+2y-1≥0\\ 3x+y-8≤0\end{array}\right.$所表示区域内任一点,则x2+y2+1的最小值为( )
| A. | $-\frac{1}{3}$ | B. | 1 | C. | 2 | D. | $-\frac{1}{2}$ |
4.已知直线l的斜率为$-\frac{{\sqrt{3}}}{3}$,则该直线l的倾斜角为( )
| A. | 30° | B. | 60° | C. | 150° | D. | 120° |
14.函数y=2016x-sinx的图象大致是( )
| A. | 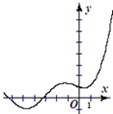 | B. | 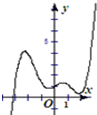 | C. | 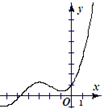 | D. | 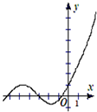 |