题目内容
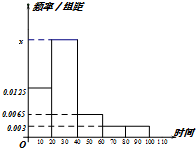 某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].(1)求直方图中x的值;
(2)如果上学路上所需时间不少于60分钟的学生可申请在学校住宿,请估计学校1000名新生中有多少名学生可以申请住宿;
(3)现有6名上学路上时间小于40分钟的新生,其中2人上学路上时间小于20分钟.从这6人中任选2人,设这2人中上学路上时间小于20分钟人数为X,求X的分布列和数学期望.
考点:离散型随机变量的期望与方差,频率分布直方图
专题:概率与统计
分析:(1)由频率分布直方图中各小矩形面积之和为1,能求出直方图中x的值.
(2)先求出新生上学所需时间不少于60分钟的频率,由此能求出1000名新生中有多少名学生可以申请住宿.
(3)由题设知X的可能取值为0,1,2,分别求出其概率,由此能求出X的分布列和数学期望.
(2)先求出新生上学所需时间不少于60分钟的频率,由此能求出1000名新生中有多少名学生可以申请住宿.
(3)由题设知X的可能取值为0,1,2,分别求出其概率,由此能求出X的分布列和数学期望.
解答:
 解:(1)由直方图可得:
解:(1)由直方图可得:
20×x+0.0125×20+0.0065×20+0.003×2×20=1.
所以 x=0.025.…(2分)
(2)新生上学所需时间不少于60分钟的频率为:
0.003×2×20=0.12…(4分)
因为1000×0.12=120
所以1000名新生中有120名学生可以申请住宿.…(6分)
(3)由题设知X的可能取值为0,1,2.…(7分)
P(X=0)=
=
,
P(X=1)=
=
,
P(X=2)=
=
,
所以X的分布列为:
…(11分)
EX=
×0+
×1+
×2=
…(12分)
 解:(1)由直方图可得:
解:(1)由直方图可得:20×x+0.0125×20+0.0065×20+0.003×2×20=1.
所以 x=0.025.…(2分)
(2)新生上学所需时间不少于60分钟的频率为:
0.003×2×20=0.12…(4分)
因为1000×0.12=120
所以1000名新生中有120名学生可以申请住宿.…(6分)
(3)由题设知X的可能取值为0,1,2.…(7分)
P(X=0)=
| ||||
|
| 2 |
| 5 |
P(X=1)=
| ||||
|
| 8 |
| 15 |
P(X=2)=
| ||||
|
| 1 |
| 15 |
所以X的分布列为:
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
EX=
| 2 |
| 5 |
| 8 |
| 15 |
| 1 |
| 15 |
| 2 |
| 3 |
点评:本题考查频率分布直方图的应用,考查离散型随机变量的分布列和数学期望,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
直线l:y=k(x-2)+2与圆C:x2+y2-2x-2y=0有两个不同的公共点,则k的取值范围是( )
| A、(一∞,一1) |
| B、(一1,1) |
| C、(一1,+∞) |
| D、(一∞,一1)∪(一1,+∞) |
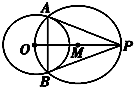 如图,已知P为⊙O外一点,以PO为直径作⊙M,⊙M交⊙O于A、B两点,求证:PA、PB是⊙O的切线.
如图,已知P为⊙O外一点,以PO为直径作⊙M,⊙M交⊙O于A、B两点,求证:PA、PB是⊙O的切线.