题目内容
设向量
=（4cosα，sinα），
=（sinβ，4cosβ），
=（cosβ，-4sinβ）．
（1）若
•
=2
•
，求tan（α+β）的值；
（2）求|
+
|的最大值；
（3）若tanαtanβ=16，求证：
∥
．
| a |
| b |
| c |
（1）若
| a |
| b |
| a |
| c |
（2）求|
| b |
| c |
（3）若tanαtanβ=16，求证：
| a |
| b |
考点：平面向量数量积坐标表示的应用
专题：三角函数的求值,平面向量及应用
分析：（1）由已知条件，利用平面向量的运算法则和三角函数的性质分别求出
•
和2
•
，再由二者相等，推导出4sin（α+β）=8cos（α+β），由此能求出tan（α+β）．
（2）先求出
+
，再利用三角函数的诱导公式和二倍角公式，能求出|
+
|的最大值．
（3）由tanαtanβ=16，化切为弦推导出
=
，由此能证明
∥
．
| a |
| b |
| a |
| c |
（2）先求出
| b |
| c |
| b |
| c |
（3）由tanαtanβ=16，化切为弦推导出
| 4cosα |
| sinβ |
| sinα |
| 4cosβ |
| a |
| b |
解答：
解：（1）∵向量
=（4cosα，sinα），
=（sinβ，4cosβ），
=（cosβ，-4sinβ），
∴
•
=4sinβcosα+4sinαcosβ=4sin（α+β），
2
•
=8cosαcosβ-8sinαsinβ=8cos（α+β），
∵
•
=2
•
，
∴4sin（α+β）=8cos（α+β），
∴tan（α+β）=
=
=2．
（2）∵
=（sinβ，4cosβ），
=（cosβ，-4sinβ），
∴|
+
|=（sinβ+cosβ，4cosβ-4sinβ）
=
=
=
，
∴当sin2β=-1时，|
+
|取最大值
=4
．
（3）∵向量
=（4cosα，sinα），
=（sinβ，4cosβ），
tanαtanβ=16，
∴
•
=16，
∴sinαsinβ=16cosαcosβ，
∴
=
，
∴
∥
．
| a |
| b |
| c |
∴
| a |
| b |
2
| a |
| c |
∵
| a |
| b |
| a |
| c |
∴4sin（α+β）=8cos（α+β），
∴tan（α+β）=
| sin(α+β) |
| cos(α+β) |
| 8 |
| 4 |
（2）∵
| b |
| c |
∴|
| b |
| c |
=
| (sinβ+cosβ)2+(4cosβ-4sinβ)2 |
=
| 17-30sinβcosβ |
=
| 17-15sin2β |
∴当sin2β=-1时，|
| b |
| c |
| 17+15 |
| 2 |
（3）∵向量
| a |
| b |
tanαtanβ=16，
∴
| sinα |
| cosα |
| sinβ |
| cosβ |
∴sinαsinβ=16cosαcosβ，
∴
| 4cosα |
| sinβ |
| sinα |
| 4cosβ |
∴
| a |
| b |
点评：本题考查向量数量积的运算，考查向量的模的最大值的求法，考查向量平行的证明，解题时要注意三角函数知识的灵活运用．
练习册系列答案
阅读快车系列答案
相关题目
已知函数g（x）是偶函数，f（x）=g（x-2），且当x≠2时其导函数f（x）满足（x-2）f′（x）＞0，若1＜a＜3，则（ ）
| A、f（4a）＜f（3）＜f（log3a） |
| B、f（3）＜f（log3a）＜f（4a） |
| C、f（log3a）＜f（3）＜f（4a） |
| D、f（log3a）＜f（4a）＜f（3） |
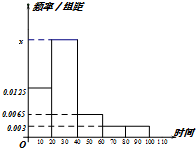某学校随机抽取部分新生调查其上学路上所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学路上所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．