题目内容
通过随机询问110名性别不同的大学生是否爱好运动，得到如下的列联表：
（1）写出x，y，z，m的值；
（2）回答能否有99%的把握认为“爱好运动与性别有关”．
附：K2=
| 男 | 女 | 总计 | |
| 爱好 | 40 | x | 60 |
| 不爱好 | y | 30 | z |
| 总计 | 60 | m | 110 |
（2）回答能否有99%的把握认为“爱好运动与性别有关”．
附：K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P（K2≥k0） | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
考点：独立性检验的应用
专题：计算题,概率与统计
分析：（1）根据2×2列联表数据之间的关系，可求x，y，z，m的值；
（2）由已知中判断爱好该项运动是否与性别有关时，由列联表中的数据此算得k2≈7.822＞6.635，而P（k2≥6.635）≈0.01，故我们有99%的把握认为爱好该项运动与性别有关．
（2）由已知中判断爱好该项运动是否与性别有关时，由列联表中的数据此算得k2≈7.822＞6.635，而P（k2≥6.635）≈0.01，故我们有99%的把握认为爱好该项运动与性别有关．
解答：
解：（1）由40+x=60，所以x=20，40+y=60，所以y=20，所以m=20+30=50，z=20+30=50；
（2）k2=
≈7.822＞6.635，
所以有99%的把握认为“爱好运动与性别有关”．
（2）k2=
| 110×(40×30-20×20)2 |
| 60×50×60×50 |
所以有99%的把握认为“爱好运动与性别有关”．
点评：本题考查独立性检验的应用，考查对于观测值表的认识，这种题目一般运算量比较大，主要要考查运算能力，本题有所创新，只要我们看出观测值对应的意义就可以，是一个基础题．
练习册系列答案
一线名师提优试卷系列答案
相关题目
已知a，b∈R．下列四个条件中，使a＞b成立的必要条件是（ ）
| A、a＞b-1 |
| B、a＞b+1 |
| C、丨a丨＞丨b丨 |
| D、a-1＞b-1 |
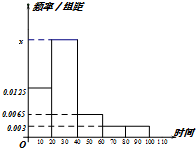某学校随机抽取部分新生调查其上学路上所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学路上所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．