题目内容
已知函数y=a-bcos(2x+
)(b>0)的最大值为3,最小值为-1.
(1)求a,b的值;
(2)当求x∈[
,
π]时,函数g(x)=4asin(bx-
)的值域.
| π |
| 6 |
(1)求a,b的值;
(2)当求x∈[
| π |
| 4 |
| 5 |
| 6 |
| π |
| 3 |
考点:函数y=Asin(ωx+φ)的图象变换,余弦函数的定义域和值域
专题:三角函数的图像与性质
分析:(1)由题意可得
,由此求得a、b的值.
(2)由(1)可得函数g(x)=4cos(2x-
),根据 x∈[
,
π],利用正弦函数的定义域和值域求得函数g(x)的值域.
|
(2)由(1)可得函数g(x)=4cos(2x-
| π |
| 3 |
| π |
| 4 |
| 5 |
| 6 |
解答:
解:(1)∵函数y=a-bcos(2x+
)(b>0)的最大值为3,最小值为-1,
∴
,解得
.
(2)由(1)可得函数g(x)=4cos(2x-
),
∵x∈[
,
π],∴2x-
∈[
,
],
∴sin(2x-
)∈[-
,1],
故函数g(x)的值域为:[-2
,4].
| π |
| 6 |
∴
|
|
(2)由(1)可得函数g(x)=4cos(2x-
| π |
| 3 |
∵x∈[
| π |
| 4 |
| 5 |
| 6 |
| π |
| 3 |
| π |
| 6 |
| 4π |
| 3 |
∴sin(2x-
| π |
| 3 |
| ||
| 2 |
故函数g(x)的值域为:[-2
| 3 |
点评:本题主要考查正弦函数、余弦函数定义域和值域,属于中档题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
设变量z,y满足约束条件
,则目标函数z=
的最大值为( )
|
| y |
| x |
A、
| ||
| B、3 | ||
| C、6 | ||
| D、9 |
将1,2,3,4四个数分为两组,每组至少一个数,则两组数的和相等的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
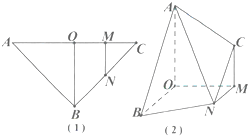 如图(1),在三角形ABC中,BA=BC=2
如图(1),在三角形ABC中,BA=BC=2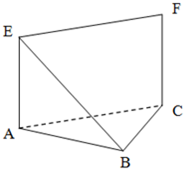 如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.
如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a. 三棱锥P-ABC中,PC、AC、BC两两垂直,BC=PC=1,AC=2,E、F、G分别是AB、AC、AP的中点.
三棱锥P-ABC中,PC、AC、BC两两垂直,BC=PC=1,AC=2,E、F、G分别是AB、AC、AP的中点.