题目内容
将1,2,3,4四个数分为两组,每组至少一个数,则两组数的和相等的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:组合及组合数公式,古典概型及其概率计算公式
专题:排列组合
分析:恰当分组,利用分类加法原理和古典概型的概率计算公式即可得出.
解答:
解:将正整数1,2,3,4随机分成两组,使得每组至少有一个数,共有分法:
+
=7种;
其中满足两组中各数之和相等的分法只有一种1,4为一组,2,3为一组,
∴两组中各数之和相等的概率P=
.
故选:B.
| C | 1 4 |
| •C | 3 3 |
| ||||
|
其中满足两组中各数之和相等的分法只有一种1,4为一组,2,3为一组,
∴两组中各数之和相等的概率P=
| 1 |
| 7 |
故选:B.
点评:本题考查古典概型及其概率计算公式,熟练掌握分类加法原理和古典概型的概率计算公式是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
下列程序语句的算法功能是( )
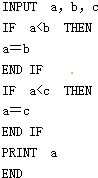
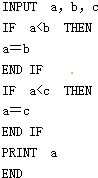
| A、输出a,b,c三个数中的最大数 |
| B、输出a,b,c三个数中的最小数 |
| C、将a,b,c按从小到大排列 |
| D、将a,b,c按从大到小排列 |
若复数(m-1)+(m-2)i(m∈R)是纯虚数,则实数m等于( )
| A、0 | B、1 | C、2 | D、1或2 |
设a=20.4,b=log20.4,则a,b的大小关系为( )
| A、a>b | B、b>a |
| C、a=b | D、不能确定 |
不等式组
在坐标平面内表示的图形的面积等于( )
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设复数z=1+
(其中i为虚数单位),则z+3
的虚部为( )
| 2 |
| i |
. |
| z |
| A、4i | B、4 | C、-4i | D、-4 |