题目内容
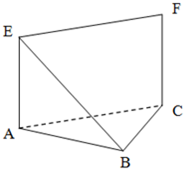 如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.
如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.(Ⅰ)求证:AB⊥平面BCF;
(Ⅱ)证明五点A、B、C、E、F在同一个球面上,并求A、F两点的球面距离.
考点:球面距离及相关计算,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)证明AB⊥平面BCF,只需证明AB⊥BC,AB⊥FC;
(Ⅱ)四边形ACFE是矩形知OA=OE=OF=OC=OB=
AF,即可证明五点A、B、C、E、F在同一个球面上,A、F两点之间的球面距离就是半个大圆的弧长,可求A、F两点的球面距离.
(Ⅱ)四边形ACFE是矩形知OA=OE=OF=OC=OB=
| 1 |
| 2 |
解答:
证明:(Ⅰ)∵∠ABC=90°,
∴AB⊥BC,
又EA⊥平面ABC,FC∥EA,∴AB⊥FC,
∵BC∩FC=C,
∴AB⊥平面BCF;
(Ⅱ)由(Ⅰ)△ABF为直角三角形,且∠ABF=90°,
记EC与AF交于点O,则由四边形ACFE是矩形知OA=OE=OF=OC=OB=
AF,
故五点A、B、C、E、F在以O为球心,AF为直径的球面上,
故A、F两点之间的球面距离就是半个大圆的弧长,是
πa.
∴AB⊥BC,
又EA⊥平面ABC,FC∥EA,∴AB⊥FC,
∵BC∩FC=C,
∴AB⊥平面BCF;
(Ⅱ)由(Ⅰ)△ABF为直角三角形,且∠ABF=90°,
记EC与AF交于点O,则由四边形ACFE是矩形知OA=OE=OF=OC=OB=
| 1 |
| 2 |
故五点A、B、C、E、F在以O为球心,AF为直径的球面上,
故A、F两点之间的球面距离就是半个大圆的弧长,是
| ||
| 2 |
点评:本题考查球面距离及相关计算,考查直线与平面垂直的判定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
设a=20.4,b=log20.4,则a,b的大小关系为( )
| A、a>b | B、b>a |
| C、a=b | D、不能确定 |
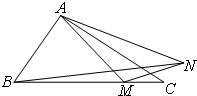 如图,已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°,
如图,已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°,