题目内容
13.I5.函数f(x)在区间(2.5755,2.5769)上有一个零点,现研究这个零点的近似值;(1)如果耍精确到0.01,那么这个近似解为2.58;
(2)如果f(2.5755)>0,f(2.5769)<0,f(2.5762)>0,并给定精确度0.001,那么这个近似解为2.576.
分析 由f(2.5755)>0,f(2.5769)<0,f(2.5762)>0,结合精确度,即可得出结论.
解答 解:(1)函数f(x)在区间(2.5755,2.5769)上有一个零点,精确到0.01,那么这个近似解为2.58,
(2)如果f(2.5755)>0,f(2.5769)<0,f(2.5762)>0,所以f(x)在区间((2.5762,2.5769)上有一个零点,
并给定精确度0.001,那么这个近似解为2.576,
故答案为:(1)2.58,(2)2.276.
点评 此题考查的是二分法求方程的近似解的问题.在解答的过程当中充分体现了同学们的运算能力以及对二分法法的应用.值得同学们体会反思.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.两平行线3x-4y-12=0与6x+ay+16=0间的距离是( )
| A. | $\frac{28}{5}$ | B. | 4 | C. | $\frac{14}{5}$ | D. | $\frac{4}{5}$ |
8.在长方体ABCD-A1B1C1D1中,AB=6,BC=4,AA1=2,P,Q分别为棱AA1,C1D1的中点,则从点P出发,沿长方体表面到达点Q的最短路径的长度为( )
| A. | 3$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | $\sqrt{34}$ | D. | 5$\sqrt{2}$ |
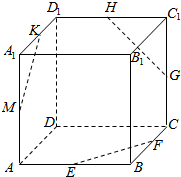 已知正方体ABCD-A1B1C1D1中,点E,F,G,H,K,M分别棱AB,BC,CC1,C1D1,A1D1,A1A的中点,如图,求证:EF,GH,KM共面.
已知正方体ABCD-A1B1C1D1中,点E,F,G,H,K,M分别棱AB,BC,CC1,C1D1,A1D1,A1A的中点,如图,求证:EF,GH,KM共面.