题目内容
4．
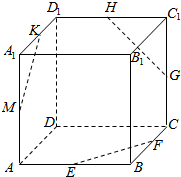已知正方体ABCD-A1B1C1D1中，点E，F，G，H，K，M分别棱AB，BC，CC1，C1D1，A1D1，A1A的中点，如图，求证：EF，GH，KM共面．
分析 利用三角形中位线定理和平行公理推导出HK∥MG∥EF，由此能证明EF，GH，KM共面．
解答 
证明：连结HK、MG、AC，
∵点E，F，G，H，K，M分别棱AB，BC，CC1，C1D1，A1D1，A1A的中点，
∴由正方体ABCD-A1B1C1D1的结构特征，得：
HK∥A1C1，A1C1∥MG∥AC，EF∥AC，
∴HK∥MG∥EF，
∴EF，GH，KM共面．
点评 本题考查三线共面的证明，是基础题，解题时要认真审题，注意三角形中位线定理和平行公理的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
14．若椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的离心率为$\frac{1}{2}$，则双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的离心率是（ ）
| A． | 2 | B． | $\frac{{\sqrt{5}}}{2}$ | C． | $\frac{{\sqrt{7}}}{2}$ | D． | 3 |
如图所示的程序框图的功能是输出a，b，c中的最小数．
将全体正整数排成一个三角形数阵：按照以上排列的规律，第n行（n≥3）从右向左的第3个数为$\frac{{{n^2}+n-4}}{2}$．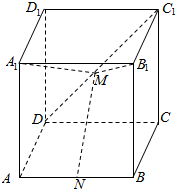
如图所示，在长方体ABCD-A1B1C1D1中，AD=1，AB=AA1=2，N、M分别是AB、C1D的中点．