题目内容
5．已知$\overrightarrow{OM}$=（1-$\frac{1}{3}$）$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$，则$\overrightarrow{AM}$=$\frac{1}{3}$$\overrightarrow{AB}$．分析 设$\overrightarrow{AM}$=k$\overrightarrow{AB}$，化为$\overrightarrow{OM}=（1-k）\overrightarrow{OA}$+k$\overrightarrow{OB}$，与$\overrightarrow{OM}$=（1-$\frac{1}{3}$）$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$比较，可得k．
解答 解：设$\overrightarrow{AM}$=k$\overrightarrow{AB}$，
则$\overrightarrow{OM}-\overrightarrow{OA}$=$k（\overrightarrow{OB}-\overrightarrow{OA}）$，
化为$\overrightarrow{OM}=（1-k）\overrightarrow{OA}$+k$\overrightarrow{OB}$，与$\overrightarrow{OM}$=（1-$\frac{1}{3}$）$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$比较，可得k=$\frac{1}{3}$，
∴$\overrightarrow{AM}$=$\frac{1}{3}$$\overrightarrow{AB}$．
故答案为：$\frac{1}{3}$．
点评 本题考查了向量共线定理、向量共面定理、向量的三角形法则，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
如图所示的程序框图的功能是输出a，b，c中的最小数．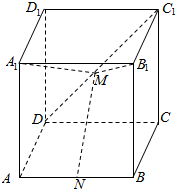
如图所示，在长方体ABCD-A1B1C1D1中，AD=1，AB=AA1=2，N、M分别是AB、C1D的中点．