已知x＞1.求y=2x+$\frac{8}{x-1}$-3的最小值及此时x的值．题目和参考答案——青夏教育精英家教网—

题目内容

1．已知x＞1，求y=2x+$\frac{8}{x-1}$-3的最小值及此时x的值．

分析变形利用基本不等式的性质即可得出．

解答解：∵x＞1，∴x-1＞0．
∴y=2x+$\frac{8}{x-1}$-3=2$[（x-1）+\frac{4}{x-1}]$-1≥2×2$\sqrt{（x-1）•\frac{4}{x-1}}$-1=7，当且仅当x=3时取等号．
∴y=2x+$\frac{8}{x-1}$-3的最小值为7，及此时x=3．

点评本题考查了基本不等式的性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案

12．

将全体正整数排成一个三角形数阵：按照以上排列的规律，第n行（n≥3）从右向左的第3个数为$\frac{{{n^2}+n-4}}{2}$．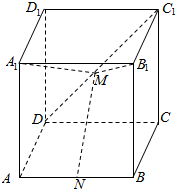

9．命题P：关于x的不等式x²+ax+1＞0对一切x∈R恒成立，命题q：方程$\frac{{x}^{2}}{a-4}$+$\frac{{y}^{2}}{a+2}$=1表示双曲线，若p∨q为真命题，p∧q为假命题，求实数a的取值范围．

16．

如图所示，在长方体ABCD-A₁B₁C₁D₁中，AD=1，AB=AA₁=2，N、M分别是AB、C₁D的中点．
（1）求证：NM∥平面A₁ADD₁；
（2）求证：NM⊥平面A₁B₁M．

6．已知圆（x-a）²+（y-b）²=r²（r＞0）与x轴，y轴都相切．则a、b、r应满足条件（　　）

13．I5．函数f（x）在区间（2.5755，2.5769）上有一个零点，现研究这个零点的近似值；
（1）如果耍精确到0.01，那么这个近似解为2.58；
（2）如果f（2.5755）＞0，f（2.5769）＜0，f（2.5762）＞0，并给定精确度0.001，那么这个近似解为2.576．

10．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），F₁，F₂为其左、右焦点，P是椭圆C上一点，PF₂⊥x轴，且sin∠PF₁F₂=$\frac{3}{5}$．
（Ⅰ）求椭圆C的离心率e；
（Ⅱ）过焦点F₂的直线l与椭圆C相交于点M、N，若△F₁MN面积的最大值为6，求椭圆C的方程．

11．已知sin（3π-α）=-2sin（$\frac{π}{2}$+α），则sinα•cosα等于$\frac{2}{5}$．

试题分类