题目内容
8.在长方体ABCD-A1B1C1D1中,AB=6,BC=4,AA1=2,P,Q分别为棱AA1,C1D1的中点,则从点P出发,沿长方体表面到达点Q的最短路径的长度为( )| A. | 3$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | $\sqrt{34}$ | D. | 5$\sqrt{2}$ |
分析 由题意画出图形,把问题转化为从小长方体PMNG-A1HQD1 的一个顶点P到另一顶点的表面最短距离问题.分类剪展求出最小值,求最小值中的最小者得答案.
解答  解:如图,
解:如图,
∵P,Q分别为棱AA1,C1D1的中点,
∴问题可转化为从小长方体PMNG-A1HQD1 的一个顶点P到另一顶点的表面最短距离问题.
共有三种剪展方法:
沿QH剪开再展开,此时最短距离为l=$\sqrt{(3+1)^{2}+{4}^{2}}=4\sqrt{2}$;
沿QN剪开再展开,此时最短距离为l=$\sqrt{(3+4)^{2}+{1}^{2}}=5\sqrt{2}$;
沿QD1 剪开再展开,此时最短距离为l=$\sqrt{(4+1)^{2}+{3}^{2}}=\sqrt{34}$.
∴从点P出发,沿长方体表面到达点Q的最短路径的长度为$4\sqrt{2}$.
故选:B.
点评 本题考查多面体表面上的最短距离问题,考查分类讨论和数形结合的解题思想方法,想到剪展的所有情况是解题的关键,是中档题.

练习册系列答案
相关题目
18.一个正方体的棱长为2cm,它的顶点都在一个球面上,则球的半径是( )cm.
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
3.设函数f(x)=|3x-1|,c<b<a,且f(c)>f(a)>f(b),则下列关系中一定成立的是( )
| A. | 3c+3a=2 | B. | 3c+3a>2 | ||
| C. | 3c+3a<2 | D. | 3c+3a与2的大小关系不确定 |
18.下列函数中,既是偶函数,周期为π的是( )
| A. | y=sin|x| | B. | y=|tanx| | C. | y=|sin2x| | D. | y=cos(2x+$\frac{x}{2}$) |
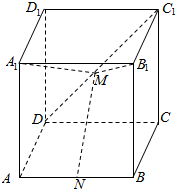 如图所示,在长方体ABCD-A1B1C1D1中,AD=1,AB=AA1=2,N、M分别是AB、C1D的中点.
如图所示,在长方体ABCD-A1B1C1D1中,AD=1,AB=AA1=2,N、M分别是AB、C1D的中点.