题目内容
已知函数f（x）=2
sinxcosx+cos2x．
（Ⅰ）求函数f（x）的最大值及相应x的取值集合；
（Ⅱ）将函数f（x）的图象向左平移
个单位得到函数g（x）的图象，试求函数g（x）的单调增区间．
| 3 |
（Ⅰ）求函数f（x）的最大值及相应x的取值集合；
（Ⅱ）将函数f（x）的图象向左平移
| π |
| 12 |
考点：函数y=Asin（ωx+φ）的图象变换,三角函数中的恒等变换应用
专题：三角函数的图像与性质
分析：（Ⅰ）利用二倍角的正弦函数以及两角和与差的三角函数化简函数的表达式，通过正弦函数的最值求函数f（x）的最大值及相应x的取值集合；
（Ⅱ）通过左加右减的原则，将函数f（x）的图象向左平移
个单位得到函数g（x）的图象，求出函数的解析式，然后利用正弦函数的单调增区间，求函数g（x）的单调增区间．
（Ⅱ）通过左加右减的原则，将函数f（x）的图象向左平移
| π |
| 12 |
解答：
解：（Ⅰ）f(x)=2(
sin2x+
cos2x)…（2分）
=2sin(2x+
)…（3分）
∴当2x+
=2kπ+
时，fmax（x）=2…（5分）
当f（x）取最大值时，x∈{x|x=kπ+
，k∈Z}…（6分）
（Ⅱ）依题意g(x)=2sin[2(x+
)+
]=2sin(2x+
)．…（9分）
∵2kπ-
≤2x+
≤2kπ+
，…（10分）
∴kπ-
≤x≤kπ+
…（11分）
故g（x）的单调增区间为[kπ-
，kπ+
]，k∈Z．…（12分）
| ||
| 2 |
| 1 |
| 2 |
=2sin(2x+
| π |
| 6 |
∴当2x+
| π |
| 6 |
| π |
| 2 |
当f（x）取最大值时，x∈{x|x=kπ+
| π |
| 6 |
（Ⅱ）依题意g(x)=2sin[2(x+
| π |
| 12 |
| π |
| 6 |
| π |
| 3 |
∵2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
∴kπ-
| 5π |
| 12 |
| π |
| 12 |
故g（x）的单调增区间为[kπ-
| 5π |
| 12 |
| π |
| 12 |
点评：本题考查三角函数的化简求值，二倍角公式的应用，考查基本知识的应用．
练习册系列答案
特高级教师点拨系列答案
相关题目
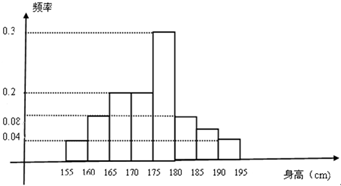现从某校高三年年级学生中随机抽取n名同学测量身高，据测量，所有学生的身高均介于155至195cm之间，将测量结果按如下方式分成8组；第一组；[155，160）；第二组[160，165）；…，第八组[190，195]．如图是按上述分组得到的条形图，其中第五组有15名同学．