题目内容
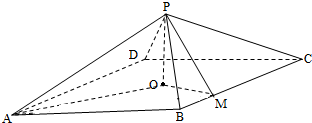 如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=
如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=| π |
| 3 |
| 1 |
| 2 |
(Ⅰ)证明:BC⊥平面POM;
(Ⅱ)若MP⊥AP,求四棱锥P-ABMO的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)连接OB,根据底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=
,M为BC上一点,且BM=
,结合菱形的性质,余弦定理,勾股定理,可得OM⊥BC及PO⊥BC,进而由线面垂直的判定定理得到BC⊥平面POM;
(Ⅱ)设PO=a,利用勾股定理和余弦定理解三角形求出PO的值,及四棱锥P-ABMO的底面积S,代入棱锥体积公式,可得答案.
| π |
| 3 |
| 1 |
| 2 |
(Ⅱ)设PO=a,利用勾股定理和余弦定理解三角形求出PO的值,及四棱锥P-ABMO的底面积S,代入棱锥体积公式,可得答案.
解答:
证明:(Ⅰ)∵底面是以O为中心的菱形,PO⊥底面ABCD,

故O为底面ABCD的中心,连接OB,则AO⊥OB,
∵AB=2,∠BAD=
,
∴OB=AB•sin∠BAO=2sin(
-
)=1,
又∵BM=
,∠OBM=
,
∴在△OBM中,OM2=OB2+BM2-2OB•BM•cos∠OBM=
,
即OB2=OM2+BM2,即OM⊥BM,
∴OM⊥BC,
又∵PO⊥底面ABCD,BC?底面ABCD,
∴PO⊥BC,
又∵OM∩PO=O,OM,PO?平面POM,
∴BC⊥平面POM;
(Ⅱ)由(Ⅰ)可得:OA=AB•cos∠BAO=2cos(
-
)=
,
设PO=a,由PO⊥底面ABCD可得:△POA为直角三角形,
故PA2=PO2+OA2=a2+3,
由△POM也为直角三角形得:
PM2=PO2+OM2=a2+
,
连接AM,
在△ABM中,AM2=AB2+BM2-2AB•BM•cos∠ABM=22+(
)2-2•2•
•cos
=
,
由MP⊥AP可知:△APM为直角三角形,
则AM2=PA2+PM2,即a2+3+a2+
=
,
解得a=
,即PO=
,
此时四棱锥P-ABMO的底面积S=S△AOB+S△BOM=
•AO•OB+
•BM•OM=
,
∴四棱锥P-ABMO的体积V=
S•PO=

故O为底面ABCD的中心,连接OB,则AO⊥OB,
∵AB=2,∠BAD=
| π |
| 3 |
∴OB=AB•sin∠BAO=2sin(
| π |
| 2 |
| π |
| 3 |
又∵BM=
| 1 |
| 2 |
| π |
| 3 |
∴在△OBM中,OM2=OB2+BM2-2OB•BM•cos∠OBM=
| 3 |
| 4 |
即OB2=OM2+BM2,即OM⊥BM,
∴OM⊥BC,
又∵PO⊥底面ABCD,BC?底面ABCD,
∴PO⊥BC,
又∵OM∩PO=O,OM,PO?平面POM,
∴BC⊥平面POM;
(Ⅱ)由(Ⅰ)可得:OA=AB•cos∠BAO=2cos(
| π |
| 2 |
| π |
| 3 |
| 3 |
设PO=a,由PO⊥底面ABCD可得:△POA为直角三角形,
故PA2=PO2+OA2=a2+3,
由△POM也为直角三角形得:
PM2=PO2+OM2=a2+
| 3 |
| 4 |
连接AM,

在△ABM中,AM2=AB2+BM2-2AB•BM•cos∠ABM=22+(
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| 3 |
| 21 |
| 4 |
由MP⊥AP可知:△APM为直角三角形,
则AM2=PA2+PM2,即a2+3+a2+
| 3 |
| 4 |
| 21 |
| 4 |
解得a=
| ||
| 2 |
| ||
| 2 |
此时四棱锥P-ABMO的底面积S=S△AOB+S△BOM=
| 1 |
| 2 |
| 1 |
| 2 |
5
| ||
| 8 |
∴四棱锥P-ABMO的体积V=
| 1 |
| 3 |
| 5 |
| 16 |
点评:本题考查的知识点是棱锥的体积,直线与平面垂直的判定,难度中档.

练习册系列答案
相关题目
直线l:y=kx+1与圆O:x2+y2=1相交于A,B 两点,则“k=1”是“△OAB的面积为
”的( )
| 1 |
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
 如图,设椭圆
如图,设椭圆