题目内容
某校早上8:00开始上课,假设该校学生小张与小王在早上7:30~7:50之间到校,且每人在该时间段的任何时刻到校是等可能的,则小张比小王至少早5分钟到校的概率为 (用数字作答).
考点:几何概型
专题:概率与统计
分析:设小张到校的时间为x,小王到校的时间为y.(x,y)可以看成平面中的点试验的全部结果所构成的区域为Ω={(x,y|30≤x≤50,30≤y≤50}是一个矩形区域,则小张比小王至少早5分钟到校事件A={(x,y)|y-x≥5}作出符合题意的图象,由图根据几何概率模型的规则求解即可.
解答:
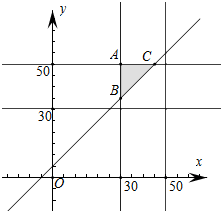 解:设小张到校的时间为x,小王到校的时间为y.(x,y)可以看成平面中的点试验的全部结果所构成的区域为Ω={(x,y|30≤x≤50,30≤y≤50}是一个矩形区域,对应的面积S=20×20=400,
解:设小张到校的时间为x,小王到校的时间为y.(x,y)可以看成平面中的点试验的全部结果所构成的区域为Ω={(x,y|30≤x≤50,30≤y≤50}是一个矩形区域,对应的面积S=20×20=400,
则小张比小王至少早5分钟到校事件A={x|y-x≥5}作出符合题意的图象,则符合题意的区域为△ABC,联立
得C(45,50),联立
得B(30,35),则S△ABC=
×15×15,由几何概率模型可知小张比小王至少早5分钟到校的概率为
=
,
故答案为:
.
 解:设小张到校的时间为x,小王到校的时间为y.(x,y)可以看成平面中的点试验的全部结果所构成的区域为Ω={(x,y|30≤x≤50,30≤y≤50}是一个矩形区域,对应的面积S=20×20=400,
解:设小张到校的时间为x,小王到校的时间为y.(x,y)可以看成平面中的点试验的全部结果所构成的区域为Ω={(x,y|30≤x≤50,30≤y≤50}是一个矩形区域,对应的面积S=20×20=400,则小张比小王至少早5分钟到校事件A={x|y-x≥5}作出符合题意的图象,则符合题意的区域为△ABC,联立
|
|
| 1 |
| 2 |
| ||
| 20×20 |
| 9 |
| 32 |
故答案为:
| 9 |
| 32 |
点评:本题考查几何概率模型与模拟方法估计概率,求解的关键是掌握两种求概率的方法的定义及规则,求出对应区域的面积是解决本题的关键.

练习册系列答案
相关题目
已知某地区中小学学生的近视情况分布如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
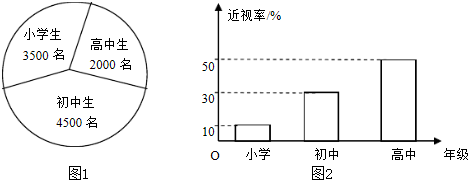

| A、200,20 |
| B、100,20 |
| C、200,10 |
| D、100,10 |
根据如下样本数据,得到回归方程
=bx+a,则( )
 |
| y |
| x | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4.0 | 2.5 | -0.5 | 0.5 | -2.0 | -3.0 |
| A、a>0,b>0 |
| B、a>0,b<0 |
| C、a<0,b>0 |
| D、a<0,b<0 |
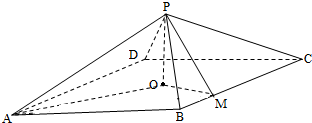 如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=
如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=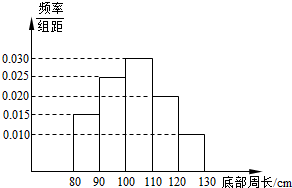 为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有
为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有