题目内容
在△ABC中,内角A、B、C所对的边分别是a、b、c,且a+b+c=8.
(Ⅰ)若a=2,b=
,求cosC的值;
(Ⅱ)若sinAcos2
+sinBcos2
=2sinC,且△ABC的面积S=
sinC,求a和b的值.
(Ⅰ)若a=2,b=
| 5 |
| 2 |
(Ⅱ)若sinAcos2
| B |
| 2 |
| A |
| 2 |
| 9 |
| 2 |
考点:余弦定理,正弦定理
专题:三角函数的求值
分析:(Ⅰ)由a+b+c=8,根据a=2,b=
求出c的长,利用余弦定理表示出cosC,将三边长代入求出cosC的值即可;
(Ⅱ)已知等式左边利用二倍角的余弦函数公式化简,整理后利用两角和与差的正弦函数公式及诱导公式变形,再利用正弦定理得到a+b=3c,与a+b+c=8联立求出a+b的值,利用三角形的面积公式列出关系式,代入S=
sinC求出ab的值,联立即可求出a与b的值.
| 5 |
| 2 |
(Ⅱ)已知等式左边利用二倍角的余弦函数公式化简,整理后利用两角和与差的正弦函数公式及诱导公式变形,再利用正弦定理得到a+b=3c,与a+b+c=8联立求出a+b的值,利用三角形的面积公式列出关系式,代入S=
| 9 |
| 2 |
解答:
解:(Ⅰ)∵a=2,b=
,且a+b+c=8,
∴c=8-(a+b)=
,
∴由余弦定理得:cosC=
=
=-
;
(Ⅱ)由sinAcos2
+sinBcos2
=2sinC可得:sinA•
+sinB•
=2sinC,
整理得:sinA+sinAcosB+sinB+sinBcosA=4sinC,
∵sinAcosB+cosAsinB=sin(A+B)=sinC,
∴sinA+sinB=3sinC,
利用正弦定理化简得:a+b=3c,
∵a+b+c=8,
∴a+b=6①,
∵S=
absinC=
sinC,
∴ab=9②,
联立①②解得:a=b=3.
| 5 |
| 2 |
∴c=8-(a+b)=
| 7 |
| 2 |
∴由余弦定理得:cosC=
| a2+b2-c2 |
| 2ab |
22+(
| ||||
2×2×
|
| 1 |
| 5 |
(Ⅱ)由sinAcos2
| B |
| 2 |
| A |
| 2 |
| 1+cosB |
| 2 |
| 1+cosA |
| 2 |
整理得:sinA+sinAcosB+sinB+sinBcosA=4sinC,
∵sinAcosB+cosAsinB=sin(A+B)=sinC,
∴sinA+sinB=3sinC,
利用正弦定理化简得:a+b=3c,
∵a+b+c=8,
∴a+b=6①,
∵S=
| 1 |
| 2 |
| 9 |
| 2 |
∴ab=9②,
联立①②解得:a=b=3.
点评:此题考查了正弦、余弦定理,以及三角形的面积公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
已知集合A={-2,0,2},B={x|x2-x-2=0},则A∩B=( )
| A、∅ | B、{2} |
| C、{0} | D、{-2} |
设点M(x0,1),若在圆O:x2+y2=1上存在点N,使得∠OMN=45°,则x0的取值范围是( )
| A、[-1,1] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|
若a>b>0,c<d<0,则一定有( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
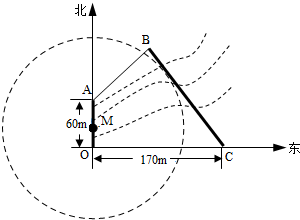 如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区,规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m,经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO=
如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区,规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m,经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO= 如图,设椭圆
如图,设椭圆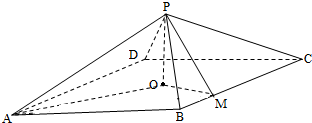 如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=
如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=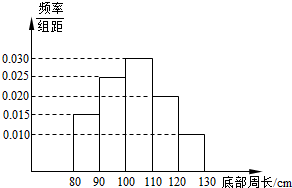 为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有
为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有