题目内容
 如图,设椭圆
如图,设椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 丨F1F2丨 |
| 丨DF1丨 |
| 2 |
| ||
| 2 |
(Ⅰ)求该椭圆的标准方程;
(Ⅱ)是否存在圆心在y轴上的圆,使圆在x轴的上方与椭圆有两个交点,且圆在这两个交点处的两条切线互相垂直并分别过不同的焦点?若存在,求出圆的方程;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设F1(-c,0),F2(c,0),依题意,可求得c=1,易求得|DF1|=
=
,|DF2|=
,从而可得2a=2
,于是可求得椭圆的标准方程;
(Ⅱ)设圆心在y轴上的圆C与椭圆
+y2=1相交,P1(x1,y1),P2(x2,y2)是两个交点,依题意,利用圆和椭圆的对称性,易知x2=-x1,y1=y2,|P1P2|=2|x1|,由F1P1⊥F2P2,得x1=-
或x1=0,分类讨论即可求得圆心及半径,从而可得圆的方程.
| |F1F2| | ||
2
|
| ||
| 2 |
3
| ||
| 2 |
| 2 |
(Ⅱ)设圆心在y轴上的圆C与椭圆
| x2 |
| 2 |
| 4 |
| 3 |
解答:
解:(Ⅰ)设F1(-c,0),F2(c,0),其中c2=a2-b2,
由
=2
,得|DF1|=
=
c,
从而S△DF1F2=
|DF1||F1F2|=
c2=
,故c=1.
从而|DF1|=
,由DF1⊥F1F2,得|DF2|2=|DF1|2+|F1F2|2=
,
因此|DF2|=
,
所以2a=|DF1|+|DF2|=2
,故a=
,b2=a2-c2=1,
因此,所求椭圆的标准方程为
+y2=1;
(Ⅱ)设圆心在y轴上的圆C与椭圆
+y2=1相交,P1(x1,y1),P2(x2,y2)是两个交点,

y1>0,y2>0,F1P1,F2P2是圆C的切线,且F1P1⊥F2P2,由圆和椭圆的对称性,易知x2=-x1,y1=y2,|P1P2|=2|x1|,
由(Ⅰ)知F1(-1,0),F2(1,0),所以
=(x1+1,y1),
=(-x1-1,y1),再由F1P1⊥F2P2,得-(x1+1)2+y12=0,
由椭圆方程得1-
=(x1+1)2,即3x12+4x1=0,解得x1=-
或x1=0.
当x1=0时,P1,P2重合,此时题设要求的圆不存在;
当x1=-
时,过P1,P2,分别与F1P1,F2P2垂直的直线的交点即为圆心C,设C(0,y0)
由F1P1,F2P2是圆C的切线,知CP1⊥F1P1,得
•
=-1,而|y1|=|x1+1|=
,
故y0=
,
故圆C的半径|CP1|=
=
.
综上,存在满足题设条件的圆,其方程为x2+(y-
)2=
.
由
| 丨F1F2丨 |
| 丨DF1丨 |
| 2 |
| |F1F2| | ||
2
|
| ||
| 2 |
从而S△DF1F2=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
从而|DF1|=
| ||
| 2 |
| 9 |
| 2 |
因此|DF2|=
3
| ||
| 2 |
所以2a=|DF1|+|DF2|=2
| 2 |
| 2 |
因此,所求椭圆的标准方程为
| x2 |
| 2 |
(Ⅱ)设圆心在y轴上的圆C与椭圆
| x2 |
| 2 |

y1>0,y2>0,F1P1,F2P2是圆C的切线,且F1P1⊥F2P2,由圆和椭圆的对称性,易知x2=-x1,y1=y2,|P1P2|=2|x1|,
由(Ⅰ)知F1(-1,0),F2(1,0),所以
| F1P1 |
| F2P2 |
由椭圆方程得1-
| x12 |
| 2 |
| 4 |
| 3 |
当x1=0时,P1,P2重合,此时题设要求的圆不存在;
当x1=-
| 4 |
| 3 |
由F1P1,F2P2是圆C的切线,知CP1⊥F1P1,得
| y1-y0 |
| x1 |
| y1 |
| x1+1 |
| 1 |
| 3 |
故y0=
| 5 |
| 3 |
故圆C的半径|CP1|=
(-
|
4
| ||
| 3 |
综上,存在满足题设条件的圆,其方程为x2+(y-
| 5 |
| 3 |
| 32 |
| 9 |
点评:本题考查直线与圆锥曲线的综合问题,考查化归思想、方程思想分类讨论思想的综合应用,考查综合分析与运算能力,属于难题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
已知集合A={-2,0,2},B={x|x2-x-2=0},则A∩B=( )
| A、∅ | B、{2} |
| C、{0} | D、{-2} |
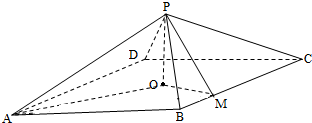 如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=
如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=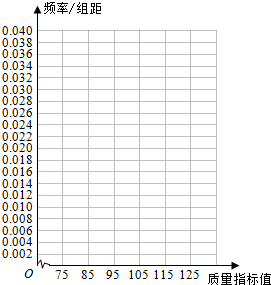
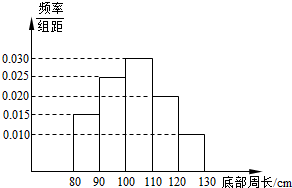 为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有
为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有