题目内容
若变量x,y满足约束条件
,则z=2x+y的最大值为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用z的几何意义,进行平移即可得到结论.
解答:
 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
由z=2x+y,得y=-2x+z,
平移直线y=-2x+z,由图象可知当直线y=-2x+z经过点C,
直线y=-2x+z的截距最大,此时z最大,
由
,解得
,即C(3,1),
此时z=2×3+1=7,
故答案为:7.
 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:由z=2x+y,得y=-2x+z,
平移直线y=-2x+z,由图象可知当直线y=-2x+z经过点C,
直线y=-2x+z的截距最大,此时z最大,
由
|
|
此时z=2×3+1=7,
故答案为:7.
点评:本题主要考查线性规划的应用,利用z的几何意义,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
设点M(x0,1),若在圆O:x2+y2=1上存在点N,使得∠OMN=45°,则x0的取值范围是( )
| A、[-1,1] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|
已知某地区中小学学生的近视情况分布如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
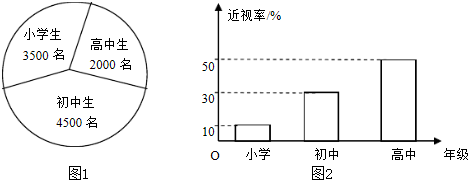

| A、200,20 |
| B、100,20 |
| C、200,10 |
| D、100,10 |
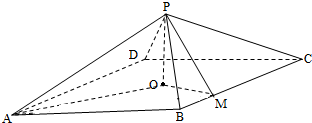 如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=
如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=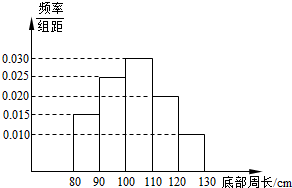 为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有
为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有