题目内容
已知{an}是首项为1,公差为2的等差数列,Sn表示{an}的前n项和.
(Ⅰ)求an及Sn;
(Ⅱ)设{bn}是首项为2的等比数列,公比为q满足q2-(a4+1)q+S4=0.求{bn}的通项公式及其前n项和Tn.
(Ⅰ)求an及Sn;
(Ⅱ)设{bn}是首项为2的等比数列,公比为q满足q2-(a4+1)q+S4=0.求{bn}的通项公式及其前n项和Tn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)直接由等差数列的通项公式及前n项和公式得答案;
(Ⅱ)求出a4和S4,代入q2-(a4+1)q+S4=0求出等比数列的公比,然后直接由等比数列的通项公式及前n项和公式得答案.
(Ⅱ)求出a4和S4,代入q2-(a4+1)q+S4=0求出等比数列的公比,然后直接由等比数列的通项公式及前n项和公式得答案.
解答:
解:(Ⅰ)∵{an}是首项为1,公差为2的等差数列,
∴an=a1+(n-1)d=1+2(n-1)=2n-1.
Sn=1+3+…+(2n-1)=
=n2;
(Ⅱ)由(Ⅰ)得,a4=7,S4=16.
∵q2-(a4+1)q+S4=0,即q2-8q+16=0,
∴(q-4)2=0,即q=4.
又∵{bn}是首项为2的等比数列,
∴bn=b1qn-1=2•4n-1=22n-1.
Tn=
=
(4n-1).
∴an=a1+(n-1)d=1+2(n-1)=2n-1.
Sn=1+3+…+(2n-1)=
| n(1+2n-1) |
| 2 |
(Ⅱ)由(Ⅰ)得,a4=7,S4=16.
∵q2-(a4+1)q+S4=0,即q2-8q+16=0,
∴(q-4)2=0,即q=4.
又∵{bn}是首项为2的等比数列,
∴bn=b1qn-1=2•4n-1=22n-1.
Tn=
| b1(1-qn) |
| 1-q |
| 2 |
| 3 |
点评:本题考查等差数列的性质,考查了等差数列和等比数列的通项公式、前n项和公式的求法,是基础题.

练习册系列答案
相关题目
设{an}是公比为q的等比数列,则“q>1”是“{an}”为递增数列的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设点M(x0,1),若在圆O:x2+y2=1上存在点N,使得∠OMN=45°,则x0的取值范围是( )
| A、[-1,1] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|
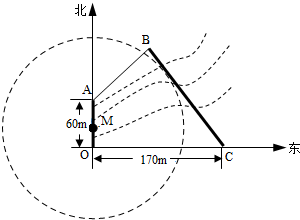 如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区,规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m,经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO=
如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区,规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m,经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO= 如图,设椭圆
如图,设椭圆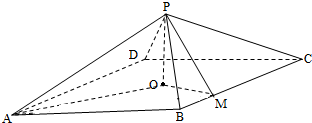 如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=
如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=