题目内容
设实数c>0,整数p>1,n∈N*.
(Ⅰ)证明:当x>-1且x≠0时,(1+x)p>1+px;
(Ⅱ)数列{an}满足a1>c
,an+1=
an+
an1-p.证明:an>an+1>c
.
(Ⅰ)证明:当x>-1且x≠0时,(1+x)p>1+px;
(Ⅱ)数列{an}满足a1>c
| 1 |
| p |
| p-1 |
| p |
| c |
| p |
| 1 |
| p |
考点:不等式的证明,数列与不等式的综合,分析法和综合法
专题:函数思想,点列、递归数列与数学归纳法
分析:第(Ⅰ)问中,可构造函数f(x)=(1+x)p-(1+px),求导数后利用函数的单调性求解;
对第(Ⅱ)问,从an+1>c
着手,由an+1=
an+
an1-p,将求证式进行等价转化后即可解决,用相同的方式将an>an+1进行转换,设法利用已证结论证明.
对第(Ⅱ)问,从an+1>c
| 1 |
| p |
| p-1 |
| p |
| c |
| p |
解答:
证明:(Ⅰ)令f(x)=(1+x)p-(1+px),则f′(x)=p(1+x)p-1-p=p[(1+x)p-1-1].
①当-1<x<0时,0<1+x<1,由p>1知p-1>0,∴(1+x)p-1<(1+x)0=1,
∴(1+x)p-1-1<0,即f′(x)<0,
∴f(x)在(-1,0]上为减函数,
∴f(x)>f(0)=(1+0)p-(1+p×0)=0,即(1+x)p-(1+px)>0,
∴(1+x)p>1+px.
②当x>0时,有1+x>1,得(1+x)p-1>(1+x)0=1,
∴f′(x)>0,
∴f(x)在[0,+∞)上为增函数,
∴f(x)>f(0)=0,
∴(1+x)p>1+px.
综合①、②知,当x>-1且x≠0时,都有(1+x)p>1+px,得证.
(Ⅱ)先证an+1>c
.
∵an+1=
an+
an1-p,∴只需证
an+
an1-p>c
,
将
写成p-1个
相加,上式左边=
an+
an+…+
an+
≥p
=c
,
当且仅当
=
,即an=c
时,上式取“=”号,
当n=1时,由题设知a1>c
,∴上式“=”号不成立,
∴
an+
an1-p>c
,即an+1>c
.
再证an>an+1.
只需证an>
an+
an1-p,化简、整理得anp>c,只需证an>c
.
由前知an+1>c
成立,即从数列{an}的第2项开始成立,
又n=1时,由题设知a1>c
成立,
∴an>c
对n∈N*成立,∴an>an+1.
综上知,an>an+1>c
,原不等式得证.
①当-1<x<0时,0<1+x<1,由p>1知p-1>0,∴(1+x)p-1<(1+x)0=1,
∴(1+x)p-1-1<0,即f′(x)<0,
∴f(x)在(-1,0]上为减函数,
∴f(x)>f(0)=(1+0)p-(1+p×0)=0,即(1+x)p-(1+px)>0,
∴(1+x)p>1+px.
②当x>0时,有1+x>1,得(1+x)p-1>(1+x)0=1,
∴f′(x)>0,
∴f(x)在[0,+∞)上为增函数,
∴f(x)>f(0)=0,
∴(1+x)p>1+px.
综合①、②知,当x>-1且x≠0时,都有(1+x)p>1+px,得证.
(Ⅱ)先证an+1>c
| 1 |
| p |
∵an+1=
| p-1 |
| p |
| c |
| p |
| p-1 |
| p |
| c |
| p |
| 1 |
| p |
将
| p-1 |
| p |
| 1 |
| p |
| 1 |
| p |
| 1 |
| p |
| 1 |
| p |
c
| ||
| p |
| p |
| ||||||||
| 1 |
| p |
当且仅当
| an |
| p |
c
| ||
| p |
| 1 |
| p |
当n=1时,由题设知a1>c
| 1 |
| p |
∴
| p-1 |
| p |
| c |
| p |
| 1 |
| p |
| 1 |
| p |
再证an>an+1.
只需证an>
| p-1 |
| p |
| c |
| p |
| 1 |
| p |
由前知an+1>c
| 1 |
| p |
又n=1时,由题设知a1>c
| 1 |
| p |
∴an>c
| 1 |
| p |
综上知,an>an+1>c
| 1 |
| p |
点评:本题是一道压轴题,考查的知识众多,涉及到函数、数列、不等式,利用的方法有分析法与综合法等,综合性很强,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设复数z满足(z-2i)(2-i)=5,则z=( )
| A、2+3i | B、2-3i |
| C、3+2i | D、3-2i |
若a>b>0,c<d<0,则一定有( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,设椭圆
如图,设椭圆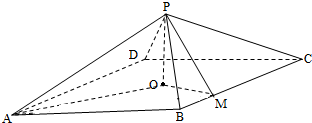 如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=
如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=