题目内容
已知函数f(x)的定义域为R,对任意实数m,n都满足 f(m+n)=f(m)+f(n)-1,当x>0时,f(x)>1,则不等式f(2x-1)+f(
)<2的解集是( )
| 1 |
| x |
A、(-∞,-
| ||
| B、(-∞,0) | ||
| C、(0,+∞) | ||
D、(-∞,-
|
考点:抽象函数及其应用
专题:函数的性质及应用
分析:令x=y=0,求出f(0)=1,令y=-x得到f(x)+f(-x)=2,令x1<x2,由条件推出f(x1)<f(x2),即可判断f(x)的单调性;
解答:
解:令x=y=0则f(0)=2f(0)-1,f(0)=1,
令y=-x,则f(0)=f(x)+f(-x)-1=1,f(x)+f(-x)=2
令x1<x2,则x2-x1>0,
∵x>0时f(x)>1
∴f(x2-x1)>1
即f(x2)+f(-x1)-1>1
∵f(-x1)+f(x1)=2
∴f(x2)-f(x1)>0即f(x1)<f(x2)
∴f(x)在R上是增函数;
f(2x-1)+f(
)=f(2x-1+
)+1
不等式f(2x-1)+f(
)<2等价于f(2x-1+
)+1<2,f(2x-1+
)<1,
∴f(2x-1+
)<f(0),
∵f(x)在R上是增函数,
∴2x-1+
<0,解得x<0,
故选:B.
令y=-x,则f(0)=f(x)+f(-x)-1=1,f(x)+f(-x)=2
令x1<x2,则x2-x1>0,
∵x>0时f(x)>1
∴f(x2-x1)>1
即f(x2)+f(-x1)-1>1
∵f(-x1)+f(x1)=2
∴f(x2)-f(x1)>0即f(x1)<f(x2)
∴f(x)在R上是增函数;
f(2x-1)+f(
| 1 |
| x |
| 1 |
| x |
不等式f(2x-1)+f(
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
∴f(2x-1+
| 1 |
| x |
∵f(x)在R上是增函数,
∴2x-1+
| 1 |
| x |
故选:B.
点评:本题主要考查函数的单调性及应用,注意定义的运用,同时考查解决抽象函数的常用方法:赋值法,务必掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
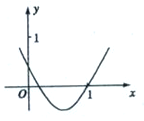 函数f(x)=x2-bx+a的图象如图所示,则函数g(x)=lnx+f′(x)的零点所在的区间是( )
函数f(x)=x2-bx+a的图象如图所示,则函数g(x)=lnx+f′(x)的零点所在的区间是( )A、(
| ||||
B、(
| ||||
| C、(1,2) | ||||
| D、(2,3) |