Question

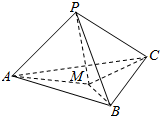如图，在三棱锥P-ABC中，PA，PB，PC两两互相垂直，且PA=3，PB=2，PC=2，设M是底面三角形ABC内一动点，定义：f（M）=（m，n，p），其中m，n，p分别表示三棱锥M-PAB，M-PBC，M-PAC的体积，若f（M）=（1，x，4y），且

1

x

+

a

y

≥8恒成立，则正实数a的最小值是（　　）

• A、2-

  2

• B、

  2 2 -1

  2

• C、

  9-4 2

  4

• D、6-4

  2

Answer 1

考点：与二面角有关的立体几何综合题

专题：空间位置关系与距离

分析：先根据三棱锥的特点求出其体积，然后利用基本不等式求出

1

x

+

a

y

的最小值，建立关于a的不等关系，解之即可．

解答： 解：∵PA、PB、PC两两垂直，且PA=3．PB=2，PC=2．
∴V _P-ABC=

1

3

×

1

2

×3×2×2=2=1+x+4y，
即x+4y=1，
∵

1

x

+

a

y

≥8恒成立，
∴

1

x

+

a

y

=（

1

x

+

a

y

）（x+4y）
=1+

ax

y

+

4y

x

+4a
≥1+4a+4

a

≥8，
解得a≥

9-4 2

4

∴正实数a的最小值为

9-4 2

4

．
故选：C．

点评：本题主要考查了棱锥的体积，同时考查了基本不等式的运用，是题意新颖的一道题目，属于中档题．