题目内容
等差数列{an}满足7a5=-5a9,且a1=-17,则使数列前n项和Sn最小的n等于 .
考点:等差数列的性质
专题:等差数列与等比数列
分析:由已知求出等差数列的公差,得到通项公式,再由通项小于0求得正整数n的值,则答案可求.
解答:
解:设等差数列{an}的公差为d,
由7a5=-5a9,且a1=-17,得:
7(-17+4d)=-5(-17+8d),得d=3.
∴an=a1+(n-1)d=-17+3(n-1)=3n-20.
由3n-20<0,得n<
,
∴当n≤6时,等差数列的项为负值.
故使数列前n项和Sn最小的n等于6.
故答案为:6.
由7a5=-5a9,且a1=-17,得:
7(-17+4d)=-5(-17+8d),得d=3.
∴an=a1+(n-1)d=-17+3(n-1)=3n-20.
由3n-20<0,得n<
| 20 |
| 3 |
∴当n≤6时,等差数列的项为负值.
故使数列前n项和Sn最小的n等于6.
故答案为:6.
点评:本题考查了等差数列的通项公式,考查了等差数列的性质,是基础的计算题.

练习册系列答案
相关题目
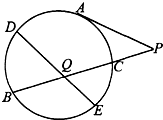 如图,PA为圆的切线,切点为A,割线PCB与圆相交于B、C两点,弦DE经过弦BC的中点Q,若AP=3
如图,PA为圆的切线,切点为A,割线PCB与圆相交于B、C两点,弦DE经过弦BC的中点Q,若AP=3
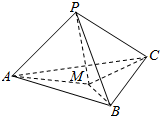 如图,在三棱锥P-ABC中,PA,PB,PC两两互相垂直,且PA=3,PB=2,PC=2,设M是底面三角形ABC内一动点,定义:f(M)=(m,n,p),其中m,n,p分别表示三棱锥M-PAB,M-PBC,M-PAC的体积,若f(M)=(1,x,4y),且
如图,在三棱锥P-ABC中,PA,PB,PC两两互相垂直,且PA=3,PB=2,PC=2,设M是底面三角形ABC内一动点,定义:f(M)=(m,n,p),其中m,n,p分别表示三棱锥M-PAB,M-PBC,M-PAC的体积,若f(M)=(1,x,4y),且