题目内容
等比数列{an}中，a5=-2，则此数列前9项的积为（ ）
| A、256 | B、-256 |
| C、-512 | D、512 |
考点：等比数列的性质
专题：等差数列与等比数列
分析：由等比数列的性质可得a1•a9=a2•a8=…=a52，进而可得数列前9项的积为T=a59，代入数据计算即可．
解答：
解：由等比数列的性质可得a1•a9=a2•a8=…=a52，
∴数列前9项的积为T=a59=（-2）9=-512
故选：C
∴数列前9项的积为T=a59=（-2）9=-512
故选：C
点评：本题考查等比数列的性质，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
双曲线x2-
=1的右焦点到准线的距离为（ ）
| y2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
在复平面内，若复数z=（x2-9）+（x-3）i为纯虚数，则实数x值为（ ）
| A、-3 | B、0 | C、3 | D、-3或3 |
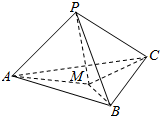如图，在三棱锥P-ABC中，PA，PB，PC两两互相垂直，且PA=3，PB=2，PC=2，设M是底面三角形ABC内一动点，定义：f（M）=（m，n，p），其中m，n，p分别表示三棱锥M-PAB，M-PBC，M-PAC的体积，若f（M）=（1，x，4y），且| 1 |
| x |
| a |
| y |
A、2-
| ||||
B、
| ||||
C、
| ||||
D、6-4
|
设点A（-2，3），B（3，1），若直线ax+y+2=0与线段AB没有交点，则a的取值范围是（ ）
A、（-∞，-
| ||
B、（-1，
| ||
C、[-
| ||
D、（-∞，-1]∪[
|
给出下列四个命题，其中错误的命题是（ ）
①若cos（A-B）cos（B-C）cos（C-A）=1，则△ABC是等边三角形
②若sinA=cosB，则△ABC是直角三角形；
③若cosAcosBcosC＜0，则△ABC是钝角三角形；
④若sin2A=sin2B，则△ABC是等腰三角形．
①若cos（A-B）cos（B-C）cos（C-A）=1，则△ABC是等边三角形
②若sinA=cosB，则△ABC是直角三角形；
③若cosAcosBcosC＜0，则△ABC是钝角三角形；
④若sin2A=sin2B，则△ABC是等腰三角形．
| A、①② | B、③④ | C、①③ | D、②④ |
在（
+
）n的二项展开式中，第三项的系数与第二项的系数的差为20，则展开式中含
的项的系数为（ ）
| x |
| 1 |
| x2 |
| 1 |
| x |
| A、8 | B、28 | C、56 | D、70 |