题目内容
设方程tan（x+
）-tan（x-
）=-2的解集为M，方程
-
=-2的解集为N，则（ ）
| π |
| 4 |
| π |
| 4 |
| 1+tanx |
| 1-tanx |
| tanx-1 |
| tanx+1 |
| A、M=N | B、M?N |
| C、N?M | D、M=Φ |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：分别求出两方程的解集确定出M与N，即可做出判断．
解答：
解：方程tan（x+
）-tan（x-
）=-2，
变形得：
-
=-2，
∴两方程相同，
则两方程解集相同，即M=N，
故选：A．
| π |
| 4 |
| π |
| 4 |
变形得：
| tanx+1 |
| 1-tanx |
| tanx-1 |
| 1+tanx |
∴两方程相同，
则两方程解集相同，即M=N，
故选：A．
点评：此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
王明早晨在6：30～7：00之间离开家去上学，送奶员在早上6：45～7：15之把牛奶送到王明家，则王明离开家之前能取到牛奶的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
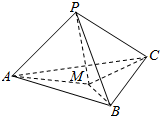如图，在三棱锥P-ABC中，PA，PB，PC两两互相垂直，且PA=3，PB=2，PC=2，设M是底面三角形ABC内一动点，定义：f（M）=（m，n，p），其中m，n，p分别表示三棱锥M-PAB，M-PBC，M-PAC的体积，若f（M）=（1，x，4y），且| 1 |
| x |
| a |
| y |
A、2-
| ||||
B、
| ||||
C、
| ||||
D、6-4
|
给出下列四个命题，其中错误的命题是（ ）
①若cos（A-B）cos（B-C）cos（C-A）=1，则△ABC是等边三角形
②若sinA=cosB，则△ABC是直角三角形；
③若cosAcosBcosC＜0，则△ABC是钝角三角形；
④若sin2A=sin2B，则△ABC是等腰三角形．
①若cos（A-B）cos（B-C）cos（C-A）=1，则△ABC是等边三角形
②若sinA=cosB，则△ABC是直角三角形；
③若cosAcosBcosC＜0，则△ABC是钝角三角形；
④若sin2A=sin2B，则△ABC是等腰三角形．
| A、①② | B、③④ | C、①③ | D、②④ |
阅读如图给出的程序框图，运行相应的程序，输出的结果S为（ ）
| A、-1007 | B、1007 |
| C、1008 | D、-3022 |
cos（-
π）的值为（ ）
| 79 |
| 6 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
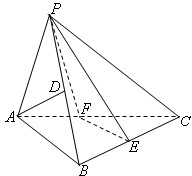在三棱锥P-ABC中，已知PA=PB，∠ABC为直角，点D，E分别为PB，BC的中点．