题目内容
已知f(x)=x-
t2+t+
为偶函数(t∈Z),且满足f(2)<f(3).
(1)求f(x)的解析式;
(2)若函数g(x)=loga[af(x)-x](a>0,且 a≠1﹚在区间[2,4]上是单调递减函数,求实数a的取值范围.
| 1 |
| 2 |
| 3 |
| 2 |
(1)求f(x)的解析式;
(2)若函数g(x)=loga[af(x)-x](a>0,且 a≠1﹚在区间[2,4]上是单调递减函数,求实数a的取值范围.
考点:复合函数的单调性,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)根据函数的奇偶性和单调性的性质,即可求出t的值,从而求f(x)的解析式;
(2)利于换元法,结合复合函数单调性之间的关系,即可得到结论.
(2)利于换元法,结合复合函数单调性之间的关系,即可得到结论.
解答:
解:(1)∵f(x)=x-
t2+t+
为偶函数(t∈Z),且满足f(2)<f(3).
∴f(x)=x-
t2+t+
在(0,+∞)上是增函数.
即-
t2+t+
>0,即t2-2t-3<0,解得-1<t<3,
∵t∈Z,∴t=0,1,2,
若t=0,则f(x)=x
为非奇非偶函数,不满足条件.
若t=1,则f(x)=x2为偶函数,满足条件.
若t=2,则f(x)=x
为非奇非偶函数,不满足条件.
故f(x)=x2.
(2)g(x)=loga[af(x)-x]=loga(ax2-x),
设t=ax2-x,则y=logat,
若g(x)=loga[af(x)-x](a>0,且 a≠1﹚在区间[2,4]上是单调递减函数,
则t=ax2-x和y=logat的单调性相反,
若a>1,则t=ax2-x在区间[2,4]上是单调递减函数,则对称轴x=-
=
≥4,即a≤
,此时不满足条件.
若0<a<1,则t=ax2-x在区间[2,4]上是单调递增函数,则对称轴x=
≤2,且当x=2时,t=4a-2>0,
解得
,即
<a<1.
| 1 |
| 2 |
| 3 |
| 2 |
∴f(x)=x-
| 1 |
| 2 |
| 3 |
| 2 |
即-
| 1 |
| 2 |
| 3 |
| 2 |
∵t∈Z,∴t=0,1,2,
若t=0,则f(x)=x
| 3 |
| 2 |
若t=1,则f(x)=x2为偶函数,满足条件.
若t=2,则f(x)=x
| 3 |
| 2 |
故f(x)=x2.
(2)g(x)=loga[af(x)-x]=loga(ax2-x),
设t=ax2-x,则y=logat,
若g(x)=loga[af(x)-x](a>0,且 a≠1﹚在区间[2,4]上是单调递减函数,
则t=ax2-x和y=logat的单调性相反,
若a>1,则t=ax2-x在区间[2,4]上是单调递减函数,则对称轴x=-
| -1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 8 |
若0<a<1,则t=ax2-x在区间[2,4]上是单调递增函数,则对称轴x=
| 1 |
| 2a |
解得
|
| 1 |
| 2 |
点评:本题主要考查函数奇偶性和单调性的应用,以及复合函数单调性之间的关系,利于换元法是解决本题的关键.

练习册系列答案
相关题目
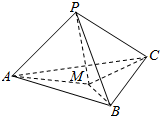 如图,在三棱锥P-ABC中,PA,PB,PC两两互相垂直,且PA=3,PB=2,PC=2,设M是底面三角形ABC内一动点,定义:f(M)=(m,n,p),其中m,n,p分别表示三棱锥M-PAB,M-PBC,M-PAC的体积,若f(M)=(1,x,4y),且
如图,在三棱锥P-ABC中,PA,PB,PC两两互相垂直,且PA=3,PB=2,PC=2,设M是底面三角形ABC内一动点,定义:f(M)=(m,n,p),其中m,n,p分别表示三棱锥M-PAB,M-PBC,M-PAC的体积,若f(M)=(1,x,4y),且| 1 |
| x |
| a |
| y |
A、2-
| ||||
B、
| ||||
C、
| ||||
D、6-4
|
cos(-
π)的值为( )
| 79 |
| 6 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
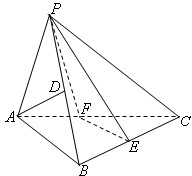 在三棱锥P-ABC中,已知PA=PB,∠ABC为直角,点D,E分别为PB,BC的中点.
在三棱锥P-ABC中,已知PA=PB,∠ABC为直角,点D,E分别为PB,BC的中点.