题目内容
已知点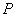 是直角坐标平面内的动点,点
是直角坐标平面内的动点,点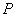 到直线
到直线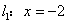 的距离为
的距离为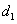 ,到点
,到点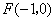 的距离为
的距离为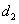 ,且
,且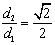 .
.
(1)求动点P所在曲线C的方程;
(2)直线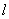 过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线
过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线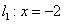 的垂线,对应的垂足分别为
的垂线,对应的垂足分别为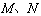 ,试判断点F与以线段
,试判断点F与以线段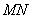 为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
(3)记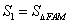 ,
,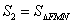 ,
,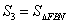 (A、B、
(A、B、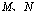 是(2)中的点),问是否存在实数
是(2)中的点),问是否存在实数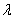 ,使
,使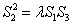 成立.若存在,求出
成立.若存在,求出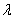 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
进一步思考问题:若上述问题中直线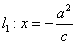 、点
、点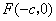 、曲线C:
、曲线C: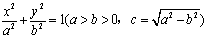 ,则使等式
,则使等式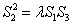 成立的
成立的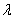 的值仍保持不变.请给出你的判断 (填写“不正确”或“正确”)(限于时间,这里不需要举反例,或证明).
的值仍保持不变.请给出你的判断 (填写“不正确”或“正确”)(限于时间,这里不需要举反例,或证明).
(1)设动点为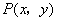 , 依据题意,有
, 依据题意,有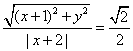 ,化简得
,化简得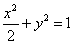 .
.
因此,动点P所在曲线C的方程是: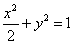 .
.
(2)点F在以MN为直径的圆的外部.
 理由:由题意可知,当过点F的直线
理由:由题意可知,当过点F的直线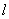 的斜率为0时,不合题意,故可设直线
的斜率为0时,不合题意,故可设直线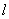 :
: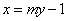 ,如图所示.
,如图所示.
联立方程组 ,可化为
,可化为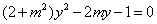 ,
,
则点 的坐标满足
的坐标满足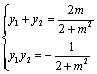 .又
.又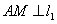 、
、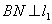 ,可得点
,可得点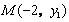 、
、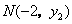 .
.
点与圆的位置关系,可以比较点到圆心的距离与半径的大小来判断,也可以计算点与直径形成的张角是锐角、直角、钝角来加以判断.
因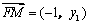 ,
,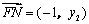 ,则
,则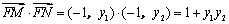 =
=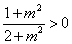 .于是,
.于是,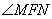 为锐角,即点F在以MN为直径的圆的外部.
为锐角,即点F在以MN为直径的圆的外部.
(3)依据(2)可算出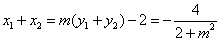 ,
,
 ,
,
则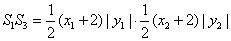

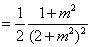 ,
,
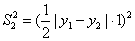
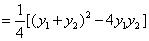
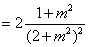 .
.
所以,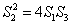 ,即存在实数
,即存在实数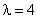 使得结论成立.对进一步思考问题的判断:正确.
使得结论成立.对进一步思考问题的判断:正确.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 与
与 互相垂直,
互相垂直, 的值为( )
的值为( ) B.
B.
 或
或
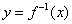 是函数
是函数 的反函数,则
的反函数,则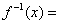 (要求写明自变量的取值范围).
(要求写明自变量的取值范围).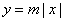 与
与 在同一坐标系的图像有公共点的充要条件是( )
在同一坐标系的图像有公共点的充要条件是( ) B.
B.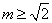 C.
C.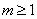 D.
D.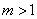
 的二元一次方程组
的二元一次方程组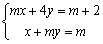 的解的情况,并说明各自的几何意义.
的解的情况,并说明各自的几何意义. 的解是_____________________.
的解是_____________________. ,若函数
,若函数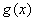 的最小正周期是
的最小正周期是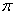 ,且当
,且当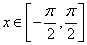 时
时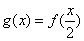 ,则关于
,则关于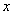 的方程
的方程 的解集为________________________.
的解集为________________________.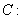
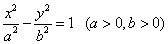 ,定义
,定义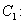
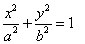 为其伴随曲线,记双曲线
为其伴随曲线,记双曲线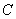 的左、右顶点为
的左、右顶点为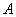 、
、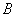 .
.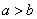 时,记双曲线
时,记双曲线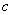 ,其伴随椭圆
,其伴随椭圆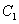 的半焦距为
的半焦距为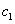 ,若
,若 ,求双曲线
,求双曲线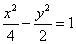 ,弦
,弦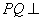
 与直线
与直线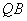 的交点为
的交点为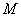 ,求动点
,求动点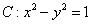 的左焦点
的左焦点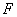 ,且斜率为
,且斜率为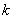 的直线
的直线 与双曲线
与双曲线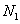 、
、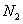 两点,求证:对任意的
两点,求证:对任意的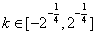 ,在伴随曲线
,在伴随曲线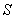 ,使得
,使得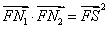 .
. cm,半径为
cm,半径为 cm,则该圆锥的体积等于
cm,则该圆锥的体积等于  .
.