题目内容
对于双曲线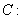
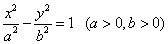 ,定义
,定义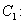
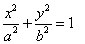 为其伴随曲线,记双曲线
为其伴随曲线,记双曲线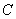 的左、右顶点为
的左、右顶点为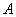 、
、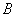 .
.
(1)当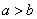 时,记双曲线
时,记双曲线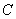 的半焦距为
的半焦距为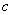 ,其伴随椭圆
,其伴随椭圆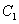 的半焦距为
的半焦距为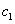 ,若
,若 ,求双曲线
,求双曲线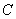 的渐近线方程;
的渐近线方程;
(2)若双曲线 的方程为
的方程为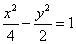 ,弦
,弦
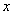 轴,记直线
轴,记直线 与直线
与直线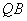 的交点为
的交点为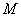 ,求动点
,求动点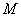 的轨迹方程;
的轨迹方程;
(3)过双曲线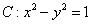 的左焦点
的左焦点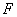 ,且斜率为
,且斜率为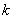 的直线
的直线 与双曲线
与双曲线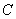 交于
交于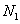 、
、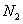 两点,求证:对任意的
两点,求证:对任意的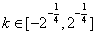 ,在伴随曲线
,在伴随曲线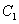 上总存在点
上总存在点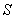 ,使得
,使得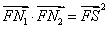 .
.
(1)∵ ,
,
由 ,得
,得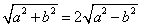 ,即
,即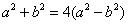 可得
可得
∴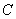 的渐近线方程为
的渐近线方程为
(2)设 ,
, ,又
,又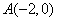 、
、 ,
,
∴直线 的方程为
的方程为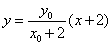 …………①
…………①
直线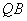 的方程为
的方程为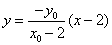 …………②
…………②
由①②得 ∵
∵  在双曲线
在双曲线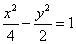 上∴
上∴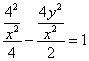 ,∴
,∴
(3)证明:点 的坐标为
的坐标为 ,直线
,直线 的方程为
的方程为 ,
,
设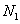 、
、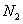 的坐标分别为
的坐标分别为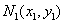 、
、
则由
 得
得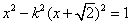 ,
,
即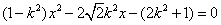 ,当
,当 时,
时,
 ∵
∵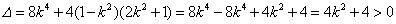
∴ ,
,


 ,由
,由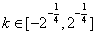 知
知  ,
,
 ∴
∴
∵双曲线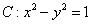 的伴随曲线是圆
的伴随曲线是圆 ,圆
,圆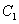 上任意一点
上任意一点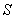 到
到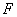 的距离
的距离 ,∴
,∴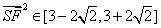
∵ ∴
∴ 对任意的
对任意的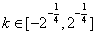 ,在伴随曲线
,在伴随曲线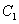 上总存在点
上总存在点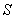 ,使得
,使得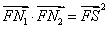

练习册系列答案
相关题目
 在点
在点 处的切线平行于
处的切线平行于 轴,则
轴,则 ___________.
___________.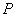 是直角坐标平面内的动点,点
是直角坐标平面内的动点,点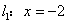 的距离为
的距离为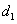 ,到点
,到点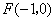 的距离为
的距离为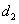 ,且
,且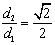 .
. 过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线
过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线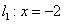 的垂线,对应的垂足分别为
的垂线,对应的垂足分别为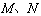 ,试判断点F与以线段
,试判断点F与以线段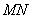 为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
为直径的圆的位置关系(指在圆内、圆上、圆外等情况);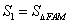 ,
,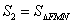 ,
,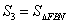 (A、B、
(A、B、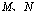 是(2)中的点),问是否存在实数
是(2)中的点),问是否存在实数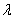 ,使
,使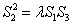 成立.若存在,求出
成立.若存在,求出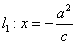 、点
、点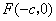 、曲线C:
、曲线C: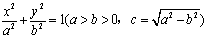 ,则使等式
,则使等式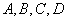 是空间四点,命题甲:
是空间四点,命题甲: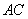 和
和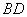 不相交,则甲是乙成立的 ( )
不相交,则甲是乙成立的 ( )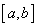 的函数
的函数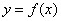 图象的两个端点为
图象的两个端点为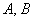 ,向量
,向量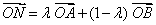 ,
, 是
是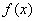 图象上任意一点,其中
图象上任意一点,其中 .若不等式
.若不等式 恒成立,则称函数
恒成立,则称函数 上函数中,线性近似阀值最小的是( )
上函数中,线性近似阀值最小的是( ) B.
B. C.
C.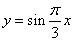 D.
D.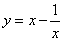
 的定义域为
的定义域为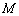 ,函数
,函数 的值域为
的值域为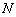 ,则
,则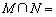 .
.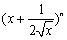 的展开式中,第4项与第7项的二项式系数相等,则展开式中
的展开式中,第4项与第7项的二项式系数相等,则展开式中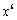 的系数为 .(用数字作答)
的系数为 .(用数字作答) 平面
平面 ,矩形
,矩形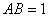 ,
,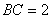 ,
, 为
为 的中点.
的中点.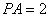 ,求异面直线
,求异面直线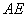 与
与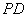 所成的角的大小.
所成的角的大小.
 中,已知
中,已知 ,则最大角等于 .
,则最大角等于 .