题目内容
3.已知椭圆$\frac{x^2}{169}+\frac{y^2}{144}=1$的两个焦点为F1、F2,椭圆上有一点P到F1的距离为10,则△PF1F2的面积为48.分析 利用椭圆的方程求出椭圆的几何量,推出2a,2b,2c;然后求解三角形的面积.
解答 解:椭圆$\frac{x^2}{169}+\frac{y^2}{144}=1$,可得a=13,b=12,c=5,由椭圆的定义可得:P到F2的距离为16,
三角形的边长分别为:10,10,16,
三角形的面积为:$\frac{1}{2}×16×\sqrt{1{0}^{2}-{8}^{2}}$=48.
故答案为:48.
点评 本题考查椭圆的简单性质,椭圆的定义的应用,考查计算能力.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
11.已知函数f(x)=2sin(2x-$\frac{π}{6}$)+a,a为常数
(1)求函数f(x)的最小正周期;
(2)若x∈[0,$\frac{π}{2}$]时,f(x)的最小值为-2,求a的值.
(1)求函数f(x)的最小正周期;
(2)若x∈[0,$\frac{π}{2}$]时,f(x)的最小值为-2,求a的值.
18.在一段时间内,某种商品的价格x(元)和需求量y(件)之间的一组数据如表所示:
(1)求出y关于x的线性回归方程;
(2)请用R2和残差图说明回归方程拟合效果的好坏.
参考数据:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\widehat{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$
参考数据:$\sum_{i=1}^5{x_i^2=1660}$,$\sum_{i=1}^5{{x_i}{y_i}}$=3992.
| 价格x/元 | 14 | 16 | 18 | 20 | 22 |
| 需求量y/件 | 56 | 50 | 3 | 1 | 37 |
(2)请用R2和残差图说明回归方程拟合效果的好坏.
参考数据:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\widehat{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$
参考数据:$\sum_{i=1}^5{x_i^2=1660}$,$\sum_{i=1}^5{{x_i}{y_i}}$=3992.
15.过正三棱柱底面一边所作的正三棱柱的截面是( )
| A. | 三角形 | B. | 三角形或梯形 | ||
| C. | 不是梯形的四边形 | D. | 梯形 |
12.已知$\overrightarrow a,\overrightarrow b$均为单位向量,它们的夹角为60°,那么|$\overrightarrow{a}$-2$\overrightarrow{b}$|等于( )
| A. | 2 | B. | $4-\sqrt{3}$ | C. | $\sqrt{13}$ | D. | $\sqrt{3}$ |
13.“x>-2”是“x2<4”( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
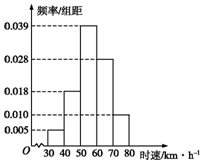 某时段内共有100辆汽车经过某一雷达地区,汽车时速的频率分布直方图如图所示,则时速不低于60km/h的汽车数量为( )
某时段内共有100辆汽车经过某一雷达地区,汽车时速的频率分布直方图如图所示,则时速不低于60km/h的汽车数量为( )