题目内容
14.已知$sin(θ+\frac{π}{3})=\frac{2}{3}$,则$cos(θ-\frac{π}{6})$=$\frac{2}{3}$.分析 由已知,利用诱导公式化简所求即可计算得解.
解答 解:∵$sin(θ+\frac{π}{3})=\frac{2}{3}$,
∴$cos(θ-\frac{π}{6})$=cos($\frac{π}{6}$-θ)=cos[$\frac{π}{2}$-($θ+\frac{π}{3}$)]=$sin(θ+\frac{π}{3})=\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题主要考查了诱导公式在三角函数化简求值中的应用,属于基础题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
4.某几何体的三视图如图所示,则该几何体的表面积为( )
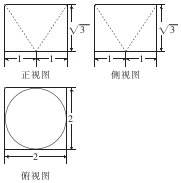

| A. | 8($\sqrt{3}$+1)+π | B. | 8($\sqrt{3}$+1)+2π | C. | 8($\sqrt{3}$+1)一π | D. | 8($\sqrt{3}$+l) |
5.顶点在原点,焦点在x轴上,且经过点P(-1,2)的拋物线的标准方程是( )
| A. | y2=$\frac{1}{4}$x | B. | y2=-$\frac{1}{4}$x | C. | y2=-4x | D. | x2=-4y |
6.已知双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0.b>0),若矩形ABCD的四个顶点在E上,AB,CD的中点为双曲线E的两个焦点,且双曲线E的离心率是2.直线AC的斜率为k.则|k|等于( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | 3 |
4.在面积为1的△ABC的边AB上任取一点P,则△PBC的面积不小于$\frac{1}{3}$的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |