题目内容
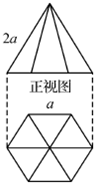 已知一个几何体的正视图和俯视图如图所示,正视图是边长为2a 的正三角形,俯视图是边长为a 的正六边形,则该几何体的侧视图的面积为( )
已知一个几何体的正视图和俯视图如图所示,正视图是边长为2a 的正三角形,俯视图是边长为a 的正六边形,则该几何体的侧视图的面积为( )A、
| ||||
B、
| ||||
| C、3a2 | ||||
D、
|
考点:简单空间图形的三视图
专题:空间位置关系与距离
分析:利用正视图与左视图的高相等,求得左视图的高,再利用俯视图与左视图的宽相等求得左视图三角形的底边长,代入三角形的面积公式计算.
解答:
解:由主视图是边长为2a的正三角形,得正六棱锥的高为
a,
∴左视图的高为
a,
∵俯视图是边长为a的正六边形,可得左视图三角形的底边长为2×
a,
∴几何体的左视图的面积S=
×
a×
a=
a2.
故选:A.
| 3 |
∴左视图的高为
| 3 |
∵俯视图是边长为a的正六边形,可得左视图三角形的底边长为2×
| ||
| 2 |
∴几何体的左视图的面积S=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
故选:A.
点评:本题考查了由几何体的正视图与俯视图求左视图的面积,根据正视图与左视图的高相等,俯视图与左视图的宽相等来求解.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
已知m、n是三次函数f(x)=
x3+
ax2+2bx(a、b∈R)的两个极值点,且m∈(0,1),n∈(1,2),则
的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
| b+3 |
| a+2 |
A、(-∞,
| ||
B、(
| ||
| C、(-4,3) | ||
| D、(-∞,-4)∪(3,+∞) |
空间四边形OABC中,OB=OC,∠AOB=∠AOC=60°,则cos<
,
>=( )
| OA |
| BC |
A、
| ||||
B、
| ||||
C、-
| ||||
| D、0 |
在(1+x)6(1+y)4的展开式中,xy2项的系数为( )
| A、45 | B、36 | C、60 | D、120 |
在数列{an}中,已知an=
(c∈R),则对于任意正整数n有( )
| n+c |
| n+1 |
| A、an<an+1 |
| B、an与an+1的大小关系和c有关 |
| C、an>an+1 |
| D、an与an+1的大小关系和n有关 |
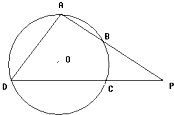 (选修4-1:几何证明选讲)如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.若AB=BC=2,则CD=
(选修4-1:几何证明选讲)如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.若AB=BC=2,则CD=