题目内容
在数列{an}中,已知an=
(c∈R),则对于任意正整数n有( )
| n+c |
| n+1 |
| A、an<an+1 |
| B、an与an+1的大小关系和c有关 |
| C、an>an+1 |
| D、an与an+1的大小关系和n有关 |
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:由
=(1+
)(1-
),可知:an与an+1的大小关系和c有关.
| an+1 |
| an |
| 1 |
| n+c |
| 1 |
| n+2 |
解答:
解:∵
=
=(1+
)(1-
),
∴an与an+1的大小关系和c有关,例如取c=0时,an=
<
=an+1;取c=1时,an=1=an+1等.
故选:B.
| an+1 |
| an |
| ||
|
| 1 |
| n+c |
| 1 |
| n+2 |
∴an与an+1的大小关系和c有关,例如取c=0时,an=
| n |
| n+1 |
| n+1 |
| n+2 |
故选:B.
点评:本题考查了数列的单调性、分类讨论思想方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
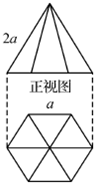 已知一个几何体的正视图和俯视图如图所示,正视图是边长为2a 的正三角形,俯视图是边长为a 的正六边形,则该几何体的侧视图的面积为( )
已知一个几何体的正视图和俯视图如图所示,正视图是边长为2a 的正三角形,俯视图是边长为a 的正六边形,则该几何体的侧视图的面积为( )A、
| ||||
B、
| ||||
| C、3a2 | ||||
D、
|
已知a,b为两条互不垂直的异面直线,a?α,b?β,下列四个结论中,不可能成立的是( )
| A、b∥α | B、b⊥α |
| C、β∥α | D、β⊥α |
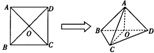 已知正方形ABCD的边长为1,AC∩BD=O,将正方形ABCD沿对角线折起,使AC=1,得到三棱锥A-BCD,如图所示.
已知正方形ABCD的边长为1,AC∩BD=O,将正方形ABCD沿对角线折起,使AC=1,得到三棱锥A-BCD,如图所示.