题目内容
若关于实数x的方程3ax2+2bx+1-a-b=0的两根可以作为一椭圆和一双曲线的离心率，则a+b的取值范围为 ．
考点：双曲线的简单性质,椭圆的简单性质
专题：不等式的解法及应用,圆锥曲线的定义、性质与方程
分析：根据椭圆的离心率大于0小于1，双曲线的离心率大于1，转化为二次方程的实根分布，结合二次函数的图象写出限制条件，解不等式即可得到．
解答：
解：由于椭圆的离心率大于0小于1，双曲线离心率大于1，
则3ax2+2bx+1-a-b=0的两根分别在（0，1）（1，+∞）上，
令g（x）=3ax2+2bx+1-a-b
则
或
，
即为
①，或
②
对于①，a＞0则-1＞2a+b＞a+b，即有a+b＜-1，
对于②，a＜0则a+b＞1．
综上可得a+b的取值范围是（-∞，-1）∪（1，+∞）．
故答案为：（-∞，-1）∪（1，+∞）．
则3ax2+2bx+1-a-b=0的两根分别在（0，1）（1，+∞）上，
令g（x）=3ax2+2bx+1-a-b
则
|
|
即为
|
|
对于①，a＞0则-1＞2a+b＞a+b，即有a+b＜-1，
对于②，a＜0则a+b＞1．
综上可得a+b的取值范围是（-∞，-1）∪（1，+∞）．
故答案为：（-∞，-1）∪（1，+∞）．
点评：本题考查圆锥曲线的离心率的范围，考查二次方程的实根分布问题，属于中档题．
练习册系列答案
相关题目
下列命题中，正确的是（ ）
A、若|
| ||||||||||||||
B、若
| ||||||||||||||
C、若（
| ||||||||||||||
D、若
|
设变量x，y满足约束条件
，则z=3x+2y的取值范围为（ ）
|
| A、（-∞，10] |
| B、[8，+∞） |
| C、[5，10] |
| D、[8，10] |
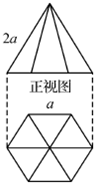已知一个几何体的正视图和俯视图如图所示，正视图是边长为2a 的正三角形，俯视图是边长为a 的正六边形，则该几何体的侧视图的面积为（ ）A、
| ||||
B、
| ||||
| C、3a2 | ||||
D、
|
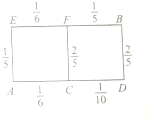某物流公司送货员从公司A处准备开车送货到某单位B处，若该地各路段发生堵车事件都是独立的，且在同一路段发生堵车事件最多只有一次，发生堵车事件的概率如图所示（例如A→C→D算作两个路段：路段AC发生堵车事件的概率为