题目内容
空间四边形OABC中,OB=OC,∠AOB=∠AOC=60°,则cos<
,
>=( )
| OA |
| BC |
A、
| ||||
B、
| ||||
C、-
| ||||
| D、0 |
考点:空间向量的夹角与距离求解公式
专题:计算题,空间向量及应用
分析:利用OB=OC,以及两个向量的数量积的定义化简计算即可得到cos<
,
>的值.
| OA |
| BC |
解答:
解:由于OB=OC,
则cos<
,
>=
=
=
=
=0,
故选D.
则cos<
| OA |
| BC |
| ||||
|
|
| ||||||
|
|
| ||||||||
|
|
=
|
| ||||||||
|
|
故选D.
点评:本题考查两个向量的数量积的定义,两个向量的夹角公式的应用,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设变量x,y满足约束条件
,则z=3x+2y的取值范围为( )
|
| A、(-∞,10] |
| B、[8,+∞) |
| C、[5,10] |
| D、[8,10] |
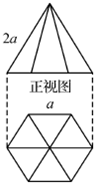 已知一个几何体的正视图和俯视图如图所示,正视图是边长为2a 的正三角形,俯视图是边长为a 的正六边形,则该几何体的侧视图的面积为( )
已知一个几何体的正视图和俯视图如图所示,正视图是边长为2a 的正三角形,俯视图是边长为a 的正六边形,则该几何体的侧视图的面积为( )A、
| ||||
B、
| ||||
| C、3a2 | ||||
D、
|
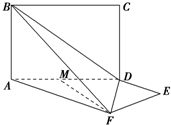 如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,M为线段AD的中点.
如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,M为线段AD的中点.