题目内容
已知
=(cosα,sinα),
=(cosβ,sinβ),且|
-
|=
.
(1)求sin(
-α)cos(2π-β)-sin(π+α)cos(β-
)的值;
(2)若cosα=
,且0<β<α<
,求β的值.
| a |
| b |
| a |
| b |
| ||
| 7 |
(1)求sin(
| π |
| 2 |
| π |
| 2 |
(2)若cosα=
| 1 |
| 7 |
| π |
| 2 |
考点:运用诱导公式化简求值,平面向量数量积的运算
专题:三角函数的求值,平面向量及应用
分析:(1)利用数量积运算性质、模的计算公式、两角和差的余弦公式即可得出;
(2)由0<β<α<
,cosα=
,可得0<α-β<
,sinα=
,sin(α-β)=
.利用sinβ=sin[α-(α-β)]=sinαcos(α-β)-cosαsin(α-β)即可得出.
(2)由0<β<α<
| π |
| 2 |
| 1 |
| 7 |
| π |
| 2 |
| 1-cos2α |
| 1-cos2(α-β) |
解答:
解:(1)∵
=(cosα,sinα),
=(cosβ,sinβ),
∴
-
=(cosα-cosβ,sinα-sinβ),
∵|
-
|=
,
∴
=
,
化为cos(α-β)=
.
∴sin(
-α)cos(2π-β)-sin(π+α)cos(β-
)=cosαcosβ+sinαsinβ=cos(α-β)=
.
(2)∵0<β<α<
,cosα=
,
∴0<α-β<
,sinα=
=
,
∴sin(α-β)=
=
.
∴sinβ=sin[α-(α-β)]
=sinαcos(α-β)-cosαsin(α-β)
=
×
-
×
=
.
∴β=
.
| a |
| b |
∴
| a |
| b |
∵|
| a |
| b |
| ||
| 7 |
∴
| (cosα-cosβ)2+(sinα-sinβ)2 |
| ||
| 7 |
化为cos(α-β)=
| 13 |
| 14 |
∴sin(
| π |
| 2 |
| π |
| 2 |
| 13 |
| 14 |
(2)∵0<β<α<
| π |
| 2 |
| 1 |
| 7 |
∴0<α-β<
| π |
| 2 |
| 1-cos2α |
4
| ||
| 7 |
∴sin(α-β)=
| 1-cos2(α-β) |
3
| ||
| 14 |
∴sinβ=sin[α-(α-β)]
=sinαcos(α-β)-cosαsin(α-β)
=
4
| ||
| 7 |
| 13 |
| 14 |
| 1 |
| 7 |
3
| ||
| 14 |
=
| ||
| 2 |
∴β=
| π |
| 3 |
点评:本题考查了数量积运算性质、模的计算公式、两角和差的正弦余弦公式、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
若一个三棱锥有三个面两两垂直,则称此三棱锥为直角三棱锥,在长方体的8个顶点中任取4个点构成的三棱锥中是直角三棱锥的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设变量x,y满足约束条件
,则z=3x+2y的取值范围为( )
|
| A、(-∞,10] |
| B、[8,+∞) |
| C、[5,10] |
| D、[8,10] |
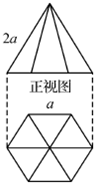 已知一个几何体的正视图和俯视图如图所示,正视图是边长为2a 的正三角形,俯视图是边长为a 的正六边形,则该几何体的侧视图的面积为( )
已知一个几何体的正视图和俯视图如图所示,正视图是边长为2a 的正三角形,俯视图是边长为a 的正六边形,则该几何体的侧视图的面积为( )A、
| ||||
B、
| ||||
| C、3a2 | ||||
D、
|