题目内容
若数列{An}满足An+1=A
,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=9,点{an,an+1}在函数f(x)=x2+2x的图象上,其中n为正整数.
(Ⅰ)证明数列{an+1}是“平方递推数列”,且数列{lg(an+1)}为等比数列;
(Ⅱ)设(Ⅰ)中“平方递推数列”的前n项积为Tn,即Tn=(a1+1)(a2+1)…(an+1),求lgTn;
(Ⅲ)在(Ⅱ)的条件下,记bn=
,求数列{bn}的前n项和Sn,并求使Sn>2014的n的最小值.
2 n |
(Ⅰ)证明数列{an+1}是“平方递推数列”,且数列{lg(an+1)}为等比数列;
(Ⅱ)设(Ⅰ)中“平方递推数列”的前n项积为Tn,即Tn=(a1+1)(a2+1)…(an+1),求lgTn;
(Ⅲ)在(Ⅱ)的条件下,记bn=
| lgTn |
| lg(an+1) |
考点:数列与不等式的综合,等比关系的确定,数列的求和
专题:等差数列与等比数列
分析:(I)由已知条件推导出an+1=
+2an,由此能证明{an+1}是“平方递推数列”,由lg(an+1+1)=2lg(an+1),能证明{lg(an+1)}是以lg(a1+1)为首项,2为公比的等比数列.
(II)解:由(I)知lg(an+1)=2n-1,由此能求出lgTn的值.
(III)由bn=
=
=2-(
)n-1,利用分组求和法能求出数列{bn}的前n项和Sn,并求出使Sn>2014的n的最小值.
| a | 2 n |
(II)解:由(I)知lg(an+1)=2n-1,由此能求出lgTn的值.
(III)由bn=
| lgTn |
| lg(an+1) |
| 2n-1 |
| 2n-1 |
| 1 |
| 2 |
解答:
(I)证明:由题意得:an+1=
+2an,
即 an+1+1=(an+1)2,
则{an+1}是“平方递推数列”,…(2分)
又有lg(an+1+1)=2lg(an+1),
得{lg(an+1)}是以lg(a1+1)为首项,2为公比的等比数列.…(4分)
(II)解:由(I)知lg(an+1)=lg(a1+1)•2n-1=2n-1,…(5分)
∴lgTn=lg(a1+1)(a2+1)…(an+1)
=lg(a1+1)+lg(a2+1)+…+lg(an+1)
=
=2n-1.…(8分)
(III)解:bn=
=
=2-(
)n-1,…(9分)
Sn=2n-
=2n-2+
,…(10分)
又Sn>2014,即2n-2+
>2014,n+
>1008,
又 0<
<1,
∴nmin=1008.…(13分)
| a | 2 n |
即 an+1+1=(an+1)2,
则{an+1}是“平方递推数列”,…(2分)
又有lg(an+1+1)=2lg(an+1),
得{lg(an+1)}是以lg(a1+1)为首项,2为公比的等比数列.…(4分)
(II)解:由(I)知lg(an+1)=lg(a1+1)•2n-1=2n-1,…(5分)
∴lgTn=lg(a1+1)(a2+1)…(an+1)
=lg(a1+1)+lg(a2+1)+…+lg(an+1)
=
| 1-2n |
| 1-2 |
(III)解:bn=
| lgTn |
| lg(an+1) |
| 2n-1 |
| 2n-1 |
| 1 |
| 2 |
Sn=2n-
1-
| ||
1-
|
| 1 |
| 2n-1 |
又Sn>2014,即2n-2+
| 1 |
| 2n-1 |
| 1 |
| 2n |
又 0<
| 1 |
| 2n |
∴nmin=1008.…(13分)
点评:本题考查平方递推数列的证明,考查等比数列的证明,考查数列的前n项和的求法及应用,解题时要认真审题,注意分组求和法的合理运用.

练习册系列答案
相关题目
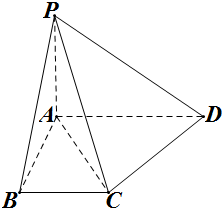 如图,直角梯形ABCD中,∠ABC=∠BAD=90°,
如图,直角梯形ABCD中,∠ABC=∠BAD=90°,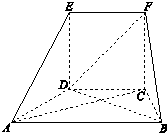 在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AC=
在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AC=