题目内容
等比数列{an}(an>0,n∈N*)中,公比q∈(0,1),a1a5+2a3a5+a2a8=25,且2是a3与a5的等比中项.
(1)求数列{an}的通项公式;
(2)设bn=log2an,数列{bn}的前n项和为Sn,
①当n为何值时,
+
+…+
有最大值,并求出最大值;
②当n≥2时,比较Sn与bn的大小.
(1)求数列{an}的通项公式;
(2)设bn=log2an,数列{bn}的前n项和为Sn,
①当n为何值时,
| S1 |
| 1 |
| S2 |
| 2 |
| Sn |
| n |
②当n≥2时,比较Sn与bn的大小.
考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:(1)根据等比数列的通项公式,建立方程组,求出首项和公比,即可求数列{an}的通项公式;
(2)求出bn=log2an的通项公式,求出数列{bn}的前n项和为Sn,即可求出
+
+…+
的最大值以及比较Sn与bn的大小.
(2)求出bn=log2an的通项公式,求出数列{bn}的前n项和为Sn,即可求出
| S1 |
| 1 |
| S2 |
| 2 |
| Sn |
| n |
解答:
解:(1)由a1a5+2a3a5+a2a8=25得(a3+a5)2=25,
∵an>0,∴a3+a5=5,又a3•a5=4,0<q<1,
∴a3=4,a5=1,从而q=
,
∴an=25-n.
(2)由(1)得bn=log2an=5-n,
∴Sn=
,即
=
,
∴{
}成等差数列,
①令
≥0,得n≤9,
∴当n=8或9时,
+
+…+
最大,最大值为8.
②Sn=
,bn=5-n,
Sn-bn=
-(5-n)=
=
,
∵n≥2,∴(ⅰ)当n>10时,Sn<bn;
(ⅱ)当n=10时,Sn=bn;
(ⅲ)当2≤n<10时,Sn>bn.
∵an>0,∴a3+a5=5,又a3•a5=4,0<q<1,
∴a3=4,a5=1,从而q=
| 1 |
| 2 |
∴an=25-n.
(2)由(1)得bn=log2an=5-n,
∴Sn=
| 9n-n2 |
| 2 |
| Sn |
| n |
| 9-n |
| 2 |
∴{
| Sn |
| n |
①令
| 9-n |
| 2 |
∴当n=8或9时,
| S1 |
| 1 |
| S2 |
| 2 |
| Sn |
| n |
②Sn=
| 9n-n2 |
| 2 |
Sn-bn=
| 9n-n2 |
| 2 |
| -n2+11n-10 |
| 2 |
| -(n-1)(n-10) |
| 2 |
∵n≥2,∴(ⅰ)当n>10时,Sn<bn;
(ⅱ)当n=10时,Sn=bn;
(ⅲ)当2≤n<10时,Sn>bn.
点评:本题主要考查等比数列的通项公式以及前n项和公式的计算,考查学生的计算能力.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
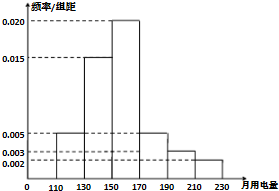 2013年第三季度,国家电网决定对城镇居民用电计费标准作出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图,如图所示.
2013年第三季度,国家电网决定对城镇居民用电计费标准作出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图,如图所示.