题目内容
已知sinα=
,cos(α-β)=
,
<β<α<π.
(1)求cos(
-2α)的值;
(2)求sinβ的值.
| ||
| 5 |
| 4 |
| 5 |
| π |
| 2 |
(1)求cos(
| 5π |
| 6 |
(2)求sinβ的值.
考点:两角和与差的余弦函数,同角三角函数间的基本关系
专题:三角函数的求值
分析:(1)由二倍角公式可得cos2α,进而可得sin2α,代入两角差的余弦公式可得;
(2)由角的范围和同角三角函数的基本关系可得cosα和sin(α-β),而sinβ=sin[α-(α-β)],展开代值计算即可.
(2)由角的范围和同角三角函数的基本关系可得cosα和sin(α-β),而sinβ=sin[α-(α-β)],展开代值计算即可.
解答:
解:(1)∵
<α<π,sinα=
<
,
∴
<α<π,∴
<2α<2π,
∴cos2α=1-2sin2α=
,
∴sin2α=-
=-
,
∴cos(
-2α)=-
cos2α+
sin2α
=-
;
(2)∵
<β<α<π,∴0<α-β<
,
又sinα=
,cos(α-β)=
,
∴cosα=-
=-
,
sin(α-β)=
=
,
∴sinβ=sin[α-(α-β)]
=sinαcos(α-β)-cosαsin(α-β)
=
×
+
×
=
.
| π |
| 2 |
| ||
| 5 |
| ||
| 2 |
∴
| 3π |
| 4 |
| 3π |
| 2 |
∴cos2α=1-2sin2α=
| 3 |
| 5 |
∴sin2α=-
| 1-cos2α |
| 4 |
| 5 |
∴cos(
| 5π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
=-
3
| ||
| 10 |
(2)∵
| π |
| 2 |
| π |
| 2 |
又sinα=
| ||
| 5 |
| 4 |
| 5 |
∴cosα=-
| 1-sin2α |
2
| ||
| 5 |
sin(α-β)=
| 1-cos2(α-β) |
| 3 |
| 5 |
∴sinβ=sin[α-(α-β)]
=sinαcos(α-β)-cosαsin(α-β)
=
| ||
| 5 |
| 4 |
| 5 |
2
| ||
| 5 |
| 3 |
| 5 |
2
| ||
| 5 |
点评:本题考查两角和与差的三角函数公式,涉及同角三角函数的基本关系,属中档题.

练习册系列答案
相关题目
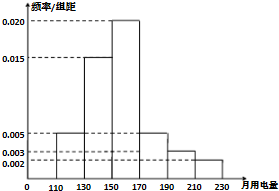 2013年第三季度,国家电网决定对城镇居民用电计费标准作出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图,如图所示.
2013年第三季度,国家电网决定对城镇居民用电计费标准作出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图,如图所示.