题目内容
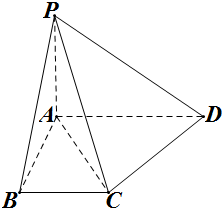 如图,直角梯形ABCD中,∠ABC=∠BAD=90°,AB=BC=
如图,直角梯形ABCD中,∠ABC=∠BAD=90°,AB=BC=| 1 |
| 2 |
(1)求证:平面PCD⊥平面PAC;
(2)侧棱PA上是否存在点E,使得BE∥平面PCD?若存在,指出E的位置并证明;若不存在请说明理由.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)由已知易得,AB,AD,AP两两垂直.分别以AB,AD,AP为x轴,y轴,z轴建立空间直角坐标系,分别求出各顶点的坐标,然后求出直线CD的方向向量及平面PAC的法向量,代入向量夹角公式,即可得到答案.
(2)设侧棱PA的中点是E,我们求出直线BE的方向向量及平面PCD的法向量,代入判断及得E点符合题目要求.
(2)设侧棱PA的中点是E,我们求出直线BE的方向向量及平面PCD的法向量,代入判断及得E点符合题目要求.
解答:
 (1)证明:∵∠PAD=90°,∴PA⊥AD.
(1)证明:∵∠PAD=90°,∴PA⊥AD.
又∵侧面PAD⊥底面ABCD,且侧面PAD∩底面ABCD=AD,
∴PA⊥底面ABCD.
又∵∠BAD=90°,∴AB,AD,AP两两垂直.
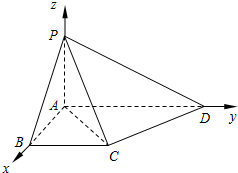
分别以AB,AD,AP为x轴,y轴,z轴建立空间直角坐标系,如图.
设AD=2,则A(0,0,0),B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,1).
∴
=(0,0,1),
=(1,1,0),
=(-1,1,0),
∴
•
=0,
•
=0,
∴AP⊥CD,AC⊥CD.
又∵AP∩AC=A,∴CD⊥平面PAC.
∵CD?平面PCD,∴平面PCD⊥平面PAC.
(2)设侧棱PA的中点是E,则E(0,0,
),
则
=(-1,0,
).
设平面PCD的一个法向量是
=(x,y,z),则
∵
=(-1,1,0),
=(0,2,-1),
∴
,取x=1,则
=(1,1,2).
∴
•
=-1+0+1=0,
∴
⊥
,
∵BE?平面PCD,∴BE∥平面PCD.
 (1)证明:∵∠PAD=90°,∴PA⊥AD.
(1)证明:∵∠PAD=90°,∴PA⊥AD.又∵侧面PAD⊥底面ABCD,且侧面PAD∩底面ABCD=AD,
∴PA⊥底面ABCD.
又∵∠BAD=90°,∴AB,AD,AP两两垂直.
分别以AB,AD,AP为x轴,y轴,z轴建立空间直角坐标系,如图.
设AD=2,则A(0,0,0),B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,1).
∴
| AP |
| AC |
| CD |
∴
| AP |
| AC |
| AC |
| CD |
∴AP⊥CD,AC⊥CD.
又∵AP∩AC=A,∴CD⊥平面PAC.
∵CD?平面PCD,∴平面PCD⊥平面PAC.
(2)设侧棱PA的中点是E,则E(0,0,
| 1 |
| 2 |
则
| BE |
| 1 |
| 2 |
设平面PCD的一个法向量是
| n |
∵
| CD |
| PD |
∴
|
| n |
∴
| n |
| BE |
∴
| n |
| BE |
∵BE?平面PCD,∴BE∥平面PCD.
点评:利用空间向量来解决立体几何夹角问题,其步骤是:建立空间直角坐标系⇒明确相关点的坐标⇒明确相关向量的坐标⇒通过空间向量的坐标运算求解.

练习册系列答案
相关题目
设物价p(元)与时间t(年)有如下关系:p(t)=(1+5%)t,那么在第10个年头,这种商品的价格上涨速度是( )
| A、10(ln1.05)9 |
| B、10ln1.05 |
| C、1.0510ln1.05 |
| D、1.0510 |
已知点P是抛物线y2=4x上一点,设点P到直线x=-1的距离为d1,到直线x+2y+10=0的距离为d2,则d1+d2的最小值是( )
| A、5 | ||||
| B、4 | ||||
C、
| ||||
D、
|
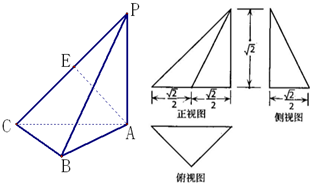 已知三棱锥P-ABC的三视图如图所示.
已知三棱锥P-ABC的三视图如图所示.