题目内容
15．
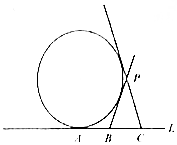如图，A，B，C是直线l上的三点，AB=4，BC=4，过A作动圆与直线l相切，过B，C分别做圆的异于l的两切线，交于点P，则P的轨迹为椭圆．（填轨迹类型，不求方程）
分析 利用切割线定理，结合椭圆的定义，即可得出结论．
解答 
解：由题意，设切点分别为D，E，则DB=4，EC=8，PE=DE
PB=4+PD，PC=8-PE，
∴PB+PC=12＞BC，
∴P的轨迹为以B，C为焦点的椭圆，
故答案为椭圆．
点评 本题考查椭圆的定义，考查切割线定理的运用，属于中档题．
练习册系列答案
相关题目
5．设椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左焦点为F，右顶点为A，点P在椭圆上，若FP⊥PA，则直线PF的斜率可以是（ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | 1 | D． | $\sqrt{3}$ |
3．已知1＜m＜4，F1，F2为曲线$C：\frac{x^2}{4}+\frac{y^2}{4-m}=1$的左、右焦点，点P为曲线C与曲线$E：{x^2}-\frac{y^2}{m-1}=1$在第一象限的交点，直线l为曲线C在点P处的切线，若三角形F1PF2的内心为点M，直线F1M与直线l交于N点，则点M，N横坐标之和为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 随m的变化而变化 |
10．在等差数列{an}中，a2=3，a14=25，则a7+a9=（ ）
| A． | 22 | B． | 75 | C． | 28 | D． | 18 |
7．已知集合A={x|y=$\sqrt{x-2}$}，B={x|x2-4＜0}，则A∪B=（ ）
| A． | ∅ | B． | （2，+∞） | C． | （-2，+∞） | D． | [0，2） |
已知四棱锥P-ABCD的直观图与三视图如图所示，其中正（主）视图与侧（左）视图为直角三角形，俯视图为正方形（数据如图所示），已知该几何体的体积为$\frac{2}{3}$．