题目内容
11.已知圆C:x2+y2+6y-a=0的圆心到直线x-y-1=0的距离等于圆C半径的$\frac{1}{2}$,则a=-1.分析 把圆的方程化为标准方程,找出圆心坐标,利用点到直线的距离公式,求出圆心到已知直线的距离,根据圆C:x2+y2+6y-a=0的圆心到直线x-y-1=0的距离等于圆C半径的$\frac{1}{2}$,求出a的值.
解答 解:把圆的方程化为标准方程得:x2+(y+3)2=a+9,
∴圆心坐标为(0,-3),
则圆心到直线x-y-1=0的距离d=$\frac{|3-1|}{\sqrt{2}}$=$\frac{1}{2}\sqrt{a+9}$,∴a=-1
故答案为-1.
点评 此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,以及点到直线的距离公式,熟练掌握距离公式是解本题的关键.

练习册系列答案
相关题目
12.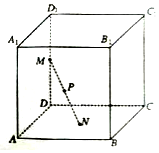 如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )
如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )
 如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )
如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{16}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{4}$ |
19.对于任意两个向量$\overrightarrow{a}$,$\overrightarrow{b}$,下列说法正确的是( )
| A. | 若$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,且$\overrightarrow{a}$与$\overrightarrow{b}$同向,则$\overrightarrow{a}$>$\overrightarrow{b}$ | B. | 当实数λ=0时,λ$\overrightarrow{a}$=0 | ||
| C. | |$\overrightarrow{a}$•$\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$| | D. | |$\overrightarrow{a}$-$\overrightarrow{b}$|≤|$\overrightarrow{a}$|-|$\overrightarrow{b}$| |
3.已知1<m<4,F1,F2为曲线$C:\frac{x^2}{4}+\frac{y^2}{4-m}=1$的左、右焦点,点P为曲线C与曲线$E:{x^2}-\frac{y^2}{m-1}=1$在第一象限的交点,直线l为曲线C在点P处的切线,若三角形F1PF2的内心为点M,直线F1M与直线l交于N点,则点M,N横坐标之和为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 随m的变化而变化 |
1.已知实数a>0,b>0,若2a+b=1,则$\frac{1}{a}+\frac{2}{b}$的最小值是( )
| A. | $\frac{8}{3}$ | B. | $\frac{11}{3}$ | C. | 4 | D. | 8 |