题目内容
6.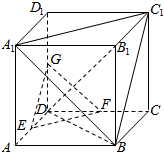 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AD、CD、DD1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AD、CD、DD1的中点.(I)证明:平面A1BC1∥平面EFG;
(Ⅱ)证明:平面BB1D1⊥平面EFG.
分析 (Ⅰ)连结CD1、CA、AD1,由已知推导出A1B∥CF、A1C1∥EF、BC1∥EG,由此能证明平面A1BC1∥平面EFG.
(Ⅱ)由已知推导出EF⊥B1D1,EF⊥BB1,由此能证明平面BB1D1⊥平面EFG.
解答 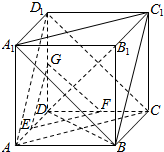 证明:(Ⅰ)连结CD1、CA、AD1,
证明:(Ⅰ)连结CD1、CA、AD1,
∵在正方体ABCD-A1B1C1D1中,E、F、G分别是AD、CD、DD1的中点,
∴GF∥CD1、EF∥CA、EG∥AD1,
∵A1B∥CD1、A1C1∥CA、BC1∥AD1,
∴A1B∥CF、A1C1∥EF、BC1∥EG,
∵CF、EF、EG两两相交,
∴平面A1BC1∥平面EFG.
(Ⅱ)∵在正方体ABCD-A1B1C1D1中,AC⊥BD,B1D1∥BD,EF∥AC,
∴EF⊥B1D1,
∵BB1⊥平面ABCD,∴EF⊥BB1,
∴EF⊥平面BB1D1,
∵EF?平面EFG,∴平面BB1D1⊥平面EFG.
点评 本题考查面面平行的证明,考查面面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
17.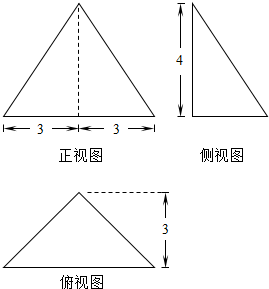 如图是某个四面体的三视图,则该四面体的外接球的表面积为( )
如图是某个四面体的三视图,则该四面体的外接球的表面积为( )
 如图是某个四面体的三视图,则该四面体的外接球的表面积为( )
如图是某个四面体的三视图,则该四面体的外接球的表面积为( )| A. | 52π | B. | 4$\sqrt{13}$π | C. | 13π | D. | $\frac{52}{3}$$\sqrt{13}$π |
18.设全集U={x∈N|-2≤x≤7},集合A={1,2,4,5},B={1,2,3,7},则∁UA∩B=( )
| A. | {1,2,3} | B. | {0,3,7} | C. | {3,7} | D. | {1,3,7} |