题目内容
15.设函数f(x)=2lnx-kx+$\frac{1}{x}$(k为常数).(1)当k=0时,求函数f(x)的最值;
(2)若k≠0,讨论函数f(x)的单调性.
分析 (1)求导,根据导数和函数的最值得关系即可求出;
(2)先求导,分类讨论即可求出函数的单调区间.
解答 解:(1)当k=0时,$f(x)=2lnx+\frac{1}{x}$,
$f'(x)=\frac{2}{x}-\frac{1}{x^2}=\frac{2x-1}{x^2}$.
函数$f(x)=2lnx+\frac{1}{x}$的定义域是(0,+∞).
令f'(x)>0,得$x>\frac{1}{2}$;令f'(x)<0,得$0<x<\frac{1}{2}$,
所以函数$f(x)=2lnx+\frac{1}{x}$在区间$({0,\frac{1}{2}})$上单调递减,在区间$({\frac{1}{2},+∞})$上单调递增.
所以函数f(x)的最小值为$f({\frac{1}{2}})=2ln\frac{1}{2}+\frac{1}{{\frac{1}{2}}}=-2ln2+2$,无最大值.
(2)函数$f(x)=2lnx-kx+\frac{1}{x}$的定义域是(0,+∞).
$f'(x)=\frac{2}{x}-k-\frac{1}{x^2}=\frac{{-k{x^2}+2x-1}}{x^2}$,
令t(x)=-kx2+2x-1,△=4-4k,
①当0<k<1时,△>0,函数t(x)=-kx2+2x-1有两个零点${x_1}=\frac{{-1-\sqrt{1-k}}}{-k}$=$\frac{{1+\sqrt{1-k}}}{k}>0$,${x_2}=\frac{{-1+\sqrt{1-k}}}{-k}$=$\frac{{1-\sqrt{1-k}}}{k}>0$,且x1>x2>0,
则f'(x)=0的两根为x1,x2.
令f'(x)>0,得x2<x<x1;
令f'(x)<0,得0<x<x2或x>x1,
所以函数f(x)在区间 ($\frac{{1-\sqrt{1-k}}}{k}$,$\frac{{1+\sqrt{1-k}}}{k}$)上单调递增,
在区间 (0,$\frac{{1-\sqrt{1-k}}}{k}$),($\frac{{1+\sqrt{1-k}}}{k},+∞$)上单调递减;
②当k≥1时,△≤0,t(x)=-kx2+2x-1≤0,f'(x)≤0,且不恒为0,所以函数f(x)在区间(0,+∞)上单调递减.
③当k<0时,△>0,
函数t(x)=-kx2+2x-1有两个零点${x_1}=\frac{{-1-\sqrt{1-k}}}{-k}$=$\frac{{1+\sqrt{1-k}}}{k}<0$(舍去),${x_2}=\frac{{-1+\sqrt{1-k}}}{-k}$=$\frac{{1-\sqrt{1-k}}}{k}>0$,
则f'(x)=0的两根为x1,x2.
令f'(x)>0,得x>x2;
令f'(x)<0,得0<x<x2,
所以函数f(x)在区间(0,$\frac{{1-\sqrt{1-k}}}{k}$)上单调递减,在区间($\frac{{1-\sqrt{1-k}}}{k},+∞$)上单调递增
点评 本题考查了导数的综合应用及存在性命题的判断,以及分类讨论的思想,属于中档题.

| A. | $\frac{f(a)}{a}$>$\frac{f(b)}{b}$>$\frac{f(c)}{c}$ | B. | $\frac{f(c)}{c}$>$\frac{f(b)}{b}$>$\frac{f(a)}{a}$ | C. | $\frac{f(b)}{b}$>$\frac{f(a)}{a}$>$\frac{f(c)}{c}$ | D. | $\frac{f(a)}{a}$>$\frac{f(c)}{c}$>$\frac{f(b)}{b}$ |
| A. | [3,+∞) | B. | (1,2] | C. | [1,4] | D. | [1,$\sqrt{2}$] |
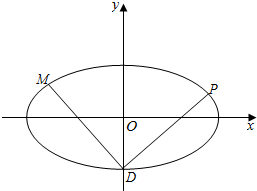 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到右准线的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到右准线的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.