题目内容
已知f(x)=x
,g(x)=
,则f(x)•g(x)= .
| x-2 |
| x-2 |
考点:函数解析式的求解及常用方法
专题:计算题,函数的性质及应用
分析:由题意,x-2≥0,从而化简f(x)•g(x)即可.
解答:
解:由题意,x-2≥0,
故x≥2;
f(x)•g(x)=x(x-2)=x2-2x,
故答案为:x2-2x,(x≥2).
故x≥2;
f(x)•g(x)=x(x-2)=x2-2x,
故答案为:x2-2x,(x≥2).
点评:本题考查了函数的解析式的求法及应用,属于基础题.

练习册系列答案
相关题目
圆(x+2)2+(y+1)2=1关于直线y=x-1对称的圆的方程为( )
| A、x2+(y-3)2=1 |
| B、x2+(y+3)2=1 |
| C、(x-3)2+y2=1 |
| D、(x+3)2+y2=1 |
函数y=
log2|x|的大致图象是( )
| x |
| |x| |
A、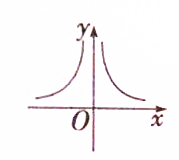 |
B、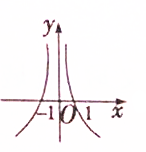 |
C、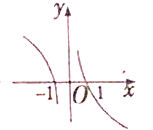 |
D、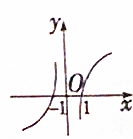 |
设i是虚数单位,若复数x满足x(1-i)=i,则其虚部为( )
A、
| ||
B、-
| ||
C、-
| ||
D、
|