题目内容
有5名同学站成一排照相，则甲与乙且甲与丙都相邻的不同排法种数是（ ）
| A、8 | B、12 | C、36 | D、48 |
考点：计数原理的应用
专题：排列组合
分析：甲与乙且甲与丙都相邻，即甲在乙丙中间，先把三人捆绑在一起，再和另外的2人全排列即可
解答：
解：甲与乙且甲与丙都相邻，即甲在乙丙中间，先把三人捆绑在一起，再和另外的2人全排列，故有
•
=12种，
故选：B
| A | 2 2 |
| A | 3 3 |
故选：B
点评：本题考查了相邻问题的站队问题，属于基础题
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
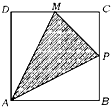如图，点P在边长为1的正方形的边上运动，设M是CD的中点，则当P沿着路径A-B-C-M运动时，点P经过的路程x与△APM的面积y的函数关系为y=f（x），则y=f（x）的图象是（ ）
A、 |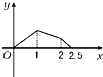
B、 |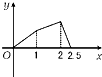
C、 |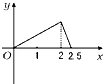
D、 |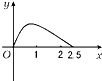
已知向量
=（-1，2），
=（m，-1），
=（3，-2），若（
-
）⊥
，则m的值是（ ）
| a |
| b |
| c |
| a |
| b |
| c |
A、
| ||
B、
| ||
| C、3 | ||
| D、-3 |