题目内容
定义在[0,+∞)的函数f(x)=ex-bx有且只有一个零点,则实数b= .
考点:函数零点的判定定理
专题:计算题,作图题,函数的性质及应用
分析:(法一)函数f(x)=ex-bx有且只有一个零点可化为y=
与y=b只有一个交点;作y=
与y=b的图象求解.(法二)利用导数确定函数的单调性,从而化简.
| ex |
| x |
| ex |
| x |
解答:
解:(法一)易知x=0不是函数f(x)=ex-bx的零点,
故函数f(x)=ex-bx有且只有一个零点可化为
y=
与y=b只有一个交点;
作y=
与y=b的图象如下,
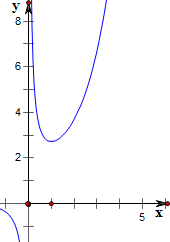
故由图象知,y=
在(0,1)上是减函数,
在(1,+∞)上是增函数,
故b=
=e;
(法二)y′=
;
故y=
在(0,1)上是减函数,
在(1,+∞)上是增函数,
从而可得b=
=e;
故答案为:e.
故函数f(x)=ex-bx有且只有一个零点可化为
y=
| ex |
| x |
作y=
| ex |
| x |

故由图象知,y=
| ex |
| x |
在(1,+∞)上是增函数,
故b=
| e |
| 1 |
(法二)y′=
| ex(x-1) |
| x2 |
故y=
| ex |
| x |
在(1,+∞)上是增函数,
从而可得b=
| e |
| 1 |
故答案为:e.
点评:本题考查了函数的零点与函数的图象的应用,属于基础题.

练习册系列答案
相关题目
有5名同学站成一排照相,则甲与乙且甲与丙都相邻的不同排法种数是( )
| A、8 | B、12 | C、36 | D、48 |
定义在R上的函数f(x)满足f(x+2)=
f(x),当x∈[0,2)时,f(x)=
函数g(x)=x3+3x2+m.若?s∈[-4,2),?t∈[-4,-2),不等式f(s)-g(t)≥0成立,则实数m的取值范围是( )
| 1 |
| 2 |
|
| A、(-∞,-12] | ||
| B、(-∞,-4] | ||
| C、(-∞,8] | ||
D、(-∞,
|
已知
、
为平面向量,若
+
与
的夹角为
,
+
与
的夹角为
,则
=( )
| a |
| b |
| a |
| b |
| a |
| π |
| 3 |
| a |
| b |
| b |
| π |
| 4 |
|
| ||
|
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若关于x的不等式x2+ax-2>0在区间[1,4]上有解,则实数a的取值范围为( )
A、(-
| ||
B、[-
| ||
| C、(1,+∞) | ||
D、(-
|
若x∈R,则“x=1”是“|x|=1”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |