Question

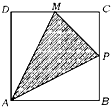如图，点P在边长为1的正方形的边上运动，设M是CD的中点，则当P沿着路径A-B-C-M运动时，点P经过的路程x与△APM的面积y的函数关系为y=f（x），则y=f（x）的图象是
（　　）

• A、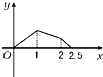
• B、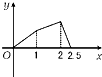
• C、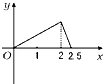
• D、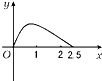

Answer 1

考点：函数的图象

专题：函数的性质及应用

分析：本题是一个分段函数，分点P在AB，BC和CM上得到三个一次函数，然后由一次函数的图象与性质确定选项．

解答： 解：①当点P在AB上时，如图：

y=

1

2

×x×1=

1

2

x（0≤x≤1）．
②当点P在BC上时，如图：

∵PB=x-1，PC=2-x，
∴y=S_{正方形ABCD}-S_△ADM-S_△ABP-S_△PCM
=1-

1

2

×

1

2

-

1

2

（x-1）-

1

2

×

1

2

×（2-x）=-

1

4

x+

3

4

，
∴y=-

1

4

x+

3

4

（1＜x≤2）
③当点P在CM上时，如图，

∵MP=2.5-x，
∴y=

1

2

（2.5-x）=-

1

2

x+

5

4

．（2＜x≤2.5）
综上①②③，得到的三个函数都是一次函数，由一次函数的图象与性质可以确定y与x的图形．
只有A的图象是三个一次函数，且在第二段上y随x的增大而减小，
故选：A．

点评：本题考查的是动点问题的函数图象，分别考虑点O在AB，BC和CM上，由三角形的面积公式得到函数的解析式．